Introdução ao Teste de Hipótese
Sendo uma metodologia muito utilizada na área de Controle Estatístico de Processo (CEP), o teste de hipótese pode ser extremamente útil quando bem aplicado para identificar quais hipóteses devem ser rejeitadas ou aceitas em um processo.
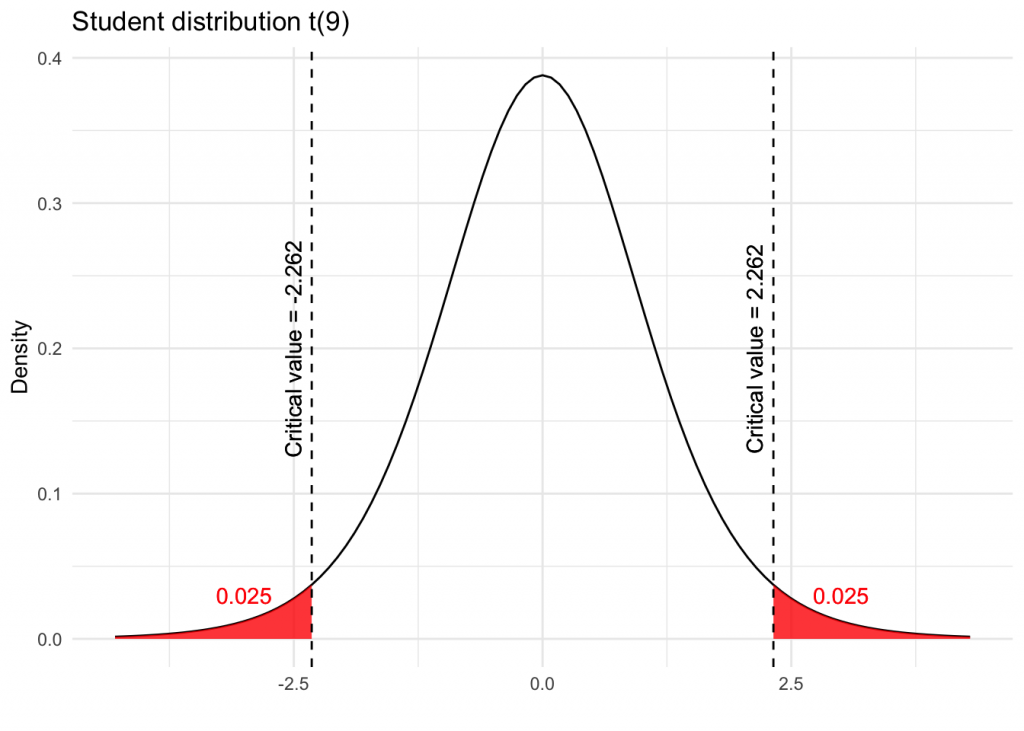
Tabela de Conteúdo
- O que é teste de hipóteses?
- O que seria o intervalo e o nível de confiança?
- Tipos de teste de hipóteses
- Erros de decisão
- Regras de decisão
- Conclusão do Teste de Hipóteses
O que é teste de hipóteses?
O teste de hipóteses, “teste de significância ou teste estatístico”, tem como principal objetivo verificar se um determinado valor hipotético representa positivamente ou não uma determinada ocasião.
É uma metodologia que auxilia nas tomadas de decisões sobre uma ou mais populações baseadas nas informações obtidas da amostra (permite verificar se os dados amostrais trazem evidências que apoiem ou não uma hipótese estatística formulada).
Ele é baseado na utilização de uma amostra aleatória extraída de uma população de interesse com a finalidade de testar uma afirmação sobre um parâmetro ou característica desta população.
Esse teste não se trata apenas de uma comparação simplificada de matemática entre dois ou mais valores, mas sim da necessidade de entender se o valor obtido a partir de uma amostra representa uma simples variação amostral da situação atual ou não.
Uma hipótese estatística é uma suposição a respeito do parâmetro populacional (essa suposição pode ou não ser verdadeira). O teste de hipóteses refere-se aos procedimentos formais utilizados pelos estatísticos para aceitar ou rejeitar essas hipóteses.
Ao tentar tomar decisões, é conveniente a formulação de suposições ou conjecturas sobre as populações de interesse, que consistem em considerações sobre parâmetros das mesmas. Essas suposições, que podem ser ou não verdadeiras, são definidas como Hipóteses Estatísticas.
Na maioria das vezes o interesse principal do pesquisador é verificar a veracidade sobre um ou mais padrões populacionais ou na distribuição direta de uma variável.
A história do Teste de Hipótese
Em 1900, o Estatístico Britânico Karl Pearson, realizou um dos primeiros testes estatísticos, o teste do Qui-quadrado, que serviu de base na comparação entre distribuição teoricamente assumida e uma distribuição de frequência.
Já o também estatístico e Britânico Ronald A Fisher foi o primeiro foi especialista em variáveis a tentar codificar e criar funções para testar hipóteses, após reunir uma série de dados, ele concluiu que as variáveis aleatórias podiam fazer parte de uma distribuição de probabilidade.
Uma outra abordagem foi estabelecida por Jerzy Neyman e Egon Pearson. Logo depois, Lehmann argumentou que de fato era possível unificar as formulações, combinando as melhores características de todas as abordagens e gerando a metodologia do teste de hipóteses.
Em qual momento utilizar o teste de hipóteses?
Os testes de hipóteses são comumente utilizados para comprovar estudos científicos, onde os resultados podem variar de uma simples hipótese nula até uma estatística mais precisa.
Para que um teste de hipótese possa ter um embasamento científico, é fundamental fazer um estudo com base nas teorias das probabilidades para determinar se uma determinada estatística está correta.
Para evitar erros, é importante que as hipóteses do teste sejam formuladas corretamente, do contrário os resultados não serão coerentes e o estudo científico não pode ser comprovado.
Para diferenciar uma hipótese alternativa de uma hipótese nula, deve-se considerar os tipos conceituais de erros e os limites padrões utilizados nos testes, desta forma, será mais fácil saber qual hipótese é a mais adequada.
Para facilitar a sua compreensão, listamos abaixo alguns casos onde utilizamos uma variável de saída contínua e uma variável de entrada:
1- Para calcular o tempo necessário para a execução de uma determinada tarefa realizada com intervalos de turnos;
2 – Análise das variações e mudanças dos equipamentos durante a produção;
3 – Para analisar a capacidade de produção de cada colaborador envolvido;
4 – Para calcular o tempo necessário para a execução de uma manutenção por planta((((((((;
5 – Para avaliar e destinar corretamente os produtos descartados pelo centro de distribuição;
6 – Para avaliar o nível de satisfação de cada cliente por item e região;
7 – Para avaliar a margem líquida dos lucros de cada produto vendido em cada departamento.
O que seria o intervalo e o nível de confiança?
Podemos definir o intervalo de confiança como os resultados obtidos durante um teste de estatísticas das amostras, onde existe uma probabilidade de que estes resultados contenham o valor de um parâmetro desconhecido.
Considerando que os dados coletados de uma amostra são feitos aleatoriamente, a probabilidade de que uma mesma população obtenha intervalos de confiança semelhantes é bem pequena. Praticamente nula.
No entanto, se estas mesmas amostras forem repetidas diversas vezes, é provável que haja uma porcentagem dos intervalos de confiança iriam conter um parâmetro desconhecido.
Nível de confiança
O nível de confiança é a porcentagem de intervalos que inclui o parâmetro populacional se forem reunidas amostras da mesma população por diversas vezes. Quando o nível de confiança é de 95%, isso normalmente indica que tudo está funcionando muito bem.
Tipos de teste de hipóteses
Existem diversos tipos de teste de hipóteses e cada um deles deve ser utilizado para conseguir atingir um objetivo específico.
Veja a seguir sobre cada um dos tipos de teste e um exemplo de sua aplicação.
Teste de hipótese tipo t para 1 amostra – Define se a média de uma amostra é diferente de maneira significativa de um valor determinado como padrão.
Teste de hipótese tipo t para 2 amostras – É responsável por determinar se a média de duas amostras independentes são diferentes de forma significativa entre si.
Teste de hipótese ANOVA – Conhecida como Análise de Variância, o teste de hipótese ANOVA é responsável por comparar a média de mais de duas amostras e determinar se uma difere significativamente da outra.
Teste de hipótese tipo t pareado – É responsável por verificar se a média de duas amostras pareadas, ou seja, dependentes, diferem de modo significativo.
Teste de hipótese para 1 proporção – Determina a proporção que uma amostra difere de maneira significativa de um valor definido como padrão.
Teste de hipóteses para 2 proporções – É responsável por comparar se a proporção de duas amostras difere significativamente.
Hipóteses nulas e alternativas
Todos os testes estatísticos são construídos com o mesmo princípio: eles se opõem a uma hipótese nula e uma hipótese alternativa.
Hipótese nula
De forma sistemática, a hipótese nula deve ser formalizada na forma de ausência de diferença e a hipótese alternativa em termos da presença de diferença.
Embora pareça simples quando você coloca dessa maneira, não é tão simples ser capaz de gerar as duas hipóteses de um teste quando você não entende para que serve o teste.
Começaremos descrevendo como a significância é determinada e o que isso significa a partir do exemplo mais simples possível.
Para compreender intuitivamente a noção de significado, vamos utilizar um exemplo bem simples, a inteligência de Albert Einstein.
Na sua opinião, ele teve uma inteligência excepcional ou uma inteligência típica da população humana?
Se você chegar à conclusão de que Albert Einstein tem inteligência excepcional, isso significa que você considera sua inteligência significativamente diferente da população em geral.
O motivo pelo qual você chega à conclusão de que Einstein é uma pessoa particularmente inteligente é que, de modo geral, você não vê muitas pessoas com uma inteligência tão elevada.
Um teste estatístico permite estimar a probabilidade de encontrar alguém tão inteligente ou mais esperto que Albert Einstein, visto que esse nível intelectual não difere do da população em geral.
A probabilidade associada a um teste estatístico para testes de hipóteses nulas é, portanto, a probabilidade de nenhuma diferença.
Como isso se traduz? Uma maneira de estimar o nível de inteligência de alguém é usar uma escala de quociente de inteligência (QI). A média desta escala é 100 e o desvio padrão é 15.
Consideramos que o nível de inteligência se distribui seguindo uma distribuição normal.
Sabendo que Einstein tinha um QI estimado de 162, pode-se calcular a probabilidade de obter um QI tão alto ou mais alto que o dele.
Em resumo, a hipótese nula (Ho) corresponde a um valor aleatório, do acaso.
Hipótese alternativa
A hipótese alternativa (H1) em geral, esta é a hipótese ‘oposta’ ou ‘contrária’ à hipótese nula.
Ele afirma que o parâmetro usado para a hipótese nula é maior, menor ou diferente
As hipóteses do tipo alternativas podem ser denominadas como unilaterais ou bilaterais.
A alternativa bilateral é utilizada para definir se o aspecto da população é maior ou menor do que o valor definido pela hipótese.
Já as hipóteses unilaterais são utilizadas para definir se o aspecto da população é diferente do valor hipotético em um caminho específico.
Com essas hipóteses é possível definir a direção sendo maior ou menor do que o valor da hipótese.
Erros de decisão
É impossível que um teste de hipótese esteja 100% certo, pois o teste é baseado em probabilidades e isso faz com que sempre haja uma possibilidade de encontrar uma conclusão errada.
Ao fazer um teste de hipóteses é possível cair no erro tipo I ou tipo II.
Ao se deparar com um desses erros é necessário definir qual é o erro que possui consequências mais graves para a situação antes de fazer a definição dos riscos.
Erro tipo I
O erro tipo I é definido como o erro que ocorre quando a hipótese nula é verdadeira, mas é rejeitada.
Erro tipo II
O erro tipo II é exatamente o contrário do que ocorre no erro tipo I. Esse tipo de erro acontece quando a hipótese nula é falsa, porém não rejeitada.
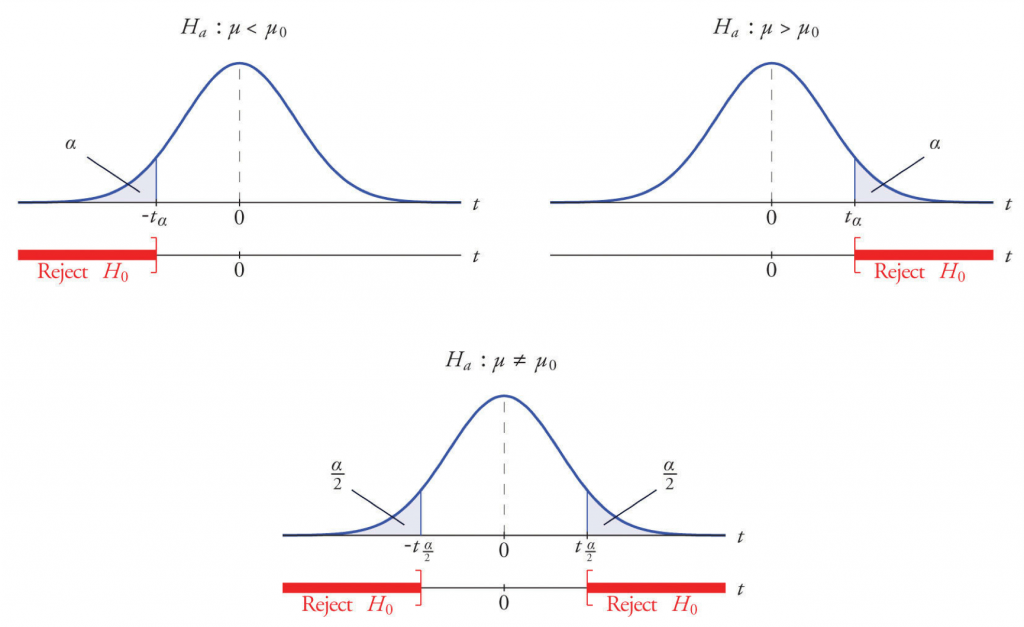
Regras de decisão
As regras de decisão fazem parte do plano de análise para rejeição de hipóteses nulas.
Tais regras podem ser feitas com base em um valor denominado como “P” ou com base em uma região de aceitação.
O valor P consiste na força de evidência em suporte para uma hipótese nula. Dessa forma, P é definido como a probabilidade de conseguirmos observar uma determinada estatística de teste tão extrema quando o S, assumindo que a hipótese seja verdadeira.
Além disso, se o valor de P for menor que S, devemos rejeitar a hipótese nula.
Já a região de aceitação consiste em um intervalo de valores, onde de forma estatística, se o teste estiver nessa região de aceitação não devemos recusar a hipótese nula.
Os intervalos de valores fora da região de aceitação estão na região de rejeição.
Etapas para fazer um teste de hipóteses
Antes de coletar os dados a serem analisados é muito importante definir os critérios para o teste e o tamanho amostral.
Existem alguns passos básicos que podem ser seguidos para fazer um teste de hipóteses.
Veja a seguir etapas básicas para conseguir configurar o teste de forma correta.
Etapa 1 – Especifique as hipóteses. É essencial garantir que as amostras estejam dentro das especificações, para isso é necessário optar pela hipótese alternativa bilateral;
Etapa 2 – Selecione um nível de significância;
Etapa 3 – Defina o poder e tamanho das amostras para o teste de hipóteses;
Etapa 4 – Faça a coleta dos dados para iniciar o teste;
Etapa 5 – Faça uma comparação do valor P ao valor do nível de significância;
Etapa 6 – Decida se deve fazer a rejeição da hipótese nula ou não.
Conclusão
O teste de hipóteses deve ser aplicado com a finalidade de selecionar a hipótese mais provável.
No entanto, quando realizamos esse tipo de teste, elaboramos a hipótese nula como a que queremos desaprovar e isso é um equívoco muito comum.
Um teste de hipótese é um processo de inferência para controlar (aceitar ou rejeitar) a partir do estudo de uma ou mais amostras aleatórias, a validade das hipóteses relativas a uma ou mais populações.
Os métodos de inferência estatística nos permitem determinar, com uma probabilidade de dados, se as diferenças observadas nas amostras podem ser atribuídas à chance ou se eles são grandes o suficiente para significar que as amostras vêm de populações provavelmente diferentes.
O teste de hipóteses envolve uma série de hipóteses sobre a natureza da população de onde vem a amostra estudada (normalidade da variável, igualdade de variâncias etc.).
Portanto, os cientistas usam testes estatísticos para determinar se a hipótese nula é verdadeira ou falsa. Se eles puderem demonstrar com alguma contingência ( probabilidade ) que a hipótese nula é falsa, então a alternativa ou hipótese de pesquisa será adotada (deve ser verdadeira).
Agora que você sabe o que é e como fazer, fica mais fácil de conseguir aplicar essa metodologia em situações do seu dia a dia.