O que é análise de regressão linear?
A regressão linear é uma ferramenta usada para dimensionar a influência de uma ou mais variáveis de entrada em uma ou mais variáveis de saída.
Como exemplo podemos trabalhar com a seguinte situação: quais são os itens (variáveis de entrada) que podem influenciar no peso de uma pessoa (variável de saída)?
Para responder esta questão podemos elencar alguns destes itens que podem interferir no peso, como consumo de doces, atividades físicas, ingestão de frituras, dieta, etc.
E aí que a regressão linear pode nos ajudar a saber quais são os itens que realmente impactam no peso, e melhor ainda, conseguimos determinar a força deste impacto e se ele é positivo (ajuda a perder peso), negativo (ajuda a ganhar peso) ou neutro (não ajuda nem atrapalha no ganho de peso).
Outro exemplo em que a regressão linear pode ser usada seria determinar se a temperatura do ambiente (clima) tem impacto na demanda por eletricidade? Será que quanto mais quente o dia haverá mais consumo de eletricidade, ou seja, mais demanda?!
Mostraremos ao longo deste texto a resposta para a pergunta acima aplicando a regressão linear simples!
Tipos de Regressão:
Há vários tipos de modelo de regressão, mas os mais comuns são:
- Regressão Linear Simples: avalia qual o impacto de uma variável de entrada sob uma variável de saída. Por exemplo: qual o impacto da temperatura (clima) sob a demanda de energia elétrica?!
- Regressão Linear Múltipla: avalia qual o impacto de mais de uma variável de entrada sob uma ou mais variáveis de saída. Por exemplo: qual o impacto da ingestão de doces e frituras sob o peso?!
- Dentre outras
Regressão Linear Simples:
Também chamada de modelo de regressão simples, avalia a influência de uma variável de entrada sobre uma variável de saída.
Para ilustrar como funciona a regressão linear simples, vamos avaliar se a temperatura do ambiente tem ou não impacto sob o consumo de energia elétrica (demanda).
Para fazer esta análise um aluno americano coletou durante 12 dias a temperatura do dia (em fahrenheit que é o padrão de medição americano, lembrando que no Brasil usamos Graus Celsius) e qual foi o consumo da energia na casa dele em kwh).
Usando a regressão conseguiremos responder as questões abaixo:
a) Há influência da temperatura sob a demanda?
b) Se houver ela é positiva ou negativa?
c) Qual a força desta influência
d) Qual a fórmula para prever a demanda?
Então vamos atrás das respostas, sendo assim gora você vai aprender como fazer uma regressão usando o Excel. Vamos fazer juntos , e para isto siga os passos:
- Abra o Excel
- Clique em “Arquivo“:
- Clique em “Opções“:
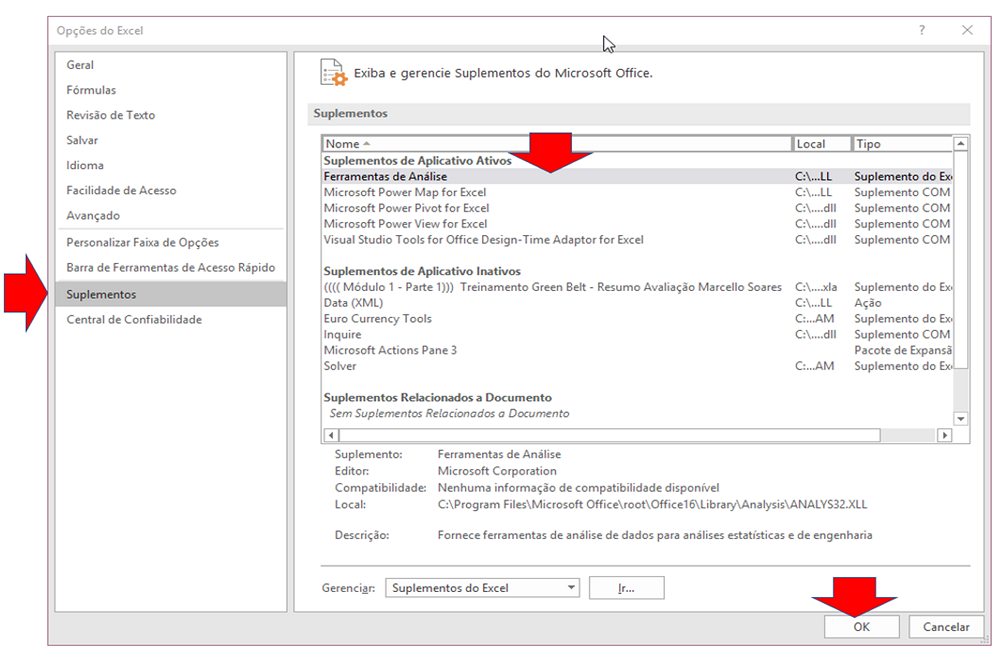
- Clicar em “Suplementos“, depois em “Ferramentas de Análise” e por fim no botão “Ok“:
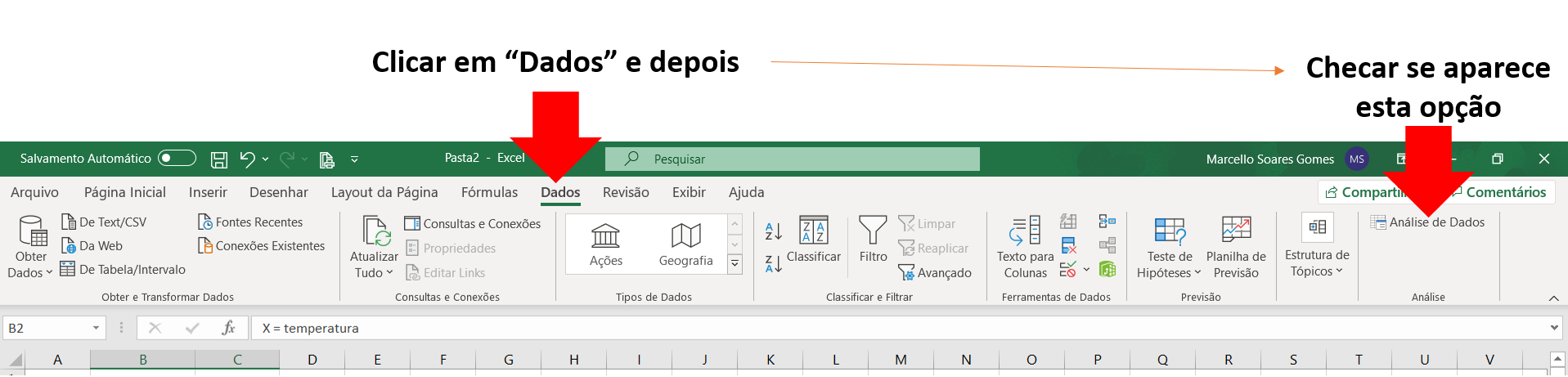
- Clique na opção “Dados” e veja se apareceu a opção “Análise de Dados“:
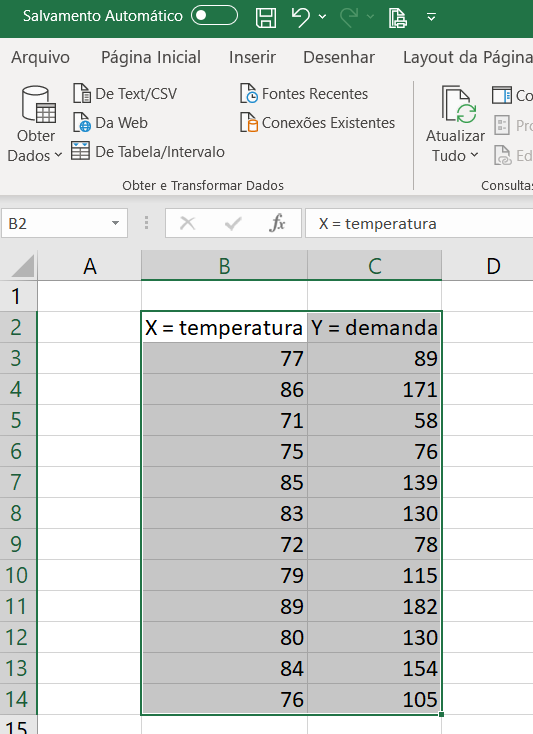
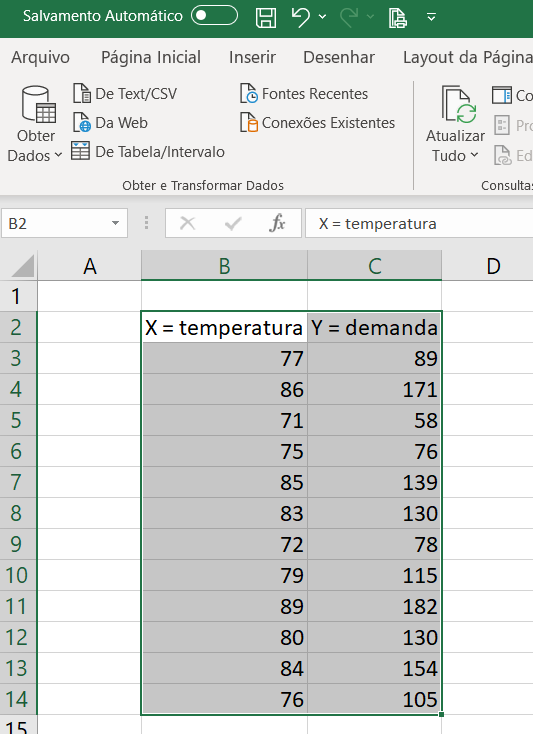
- Digite os dados abaixo no Excel, como mostrado abaixo, sendo que o X é a temperatura que o aluno americano coletou e que é dada em fahrenheit e o Y é a demanda, ou seja, quantos kwh foram consumidos.
Digite os dados exatamente nas células mostradas abaixo, ou seja, inicie na célula B2 da planilha Excel:
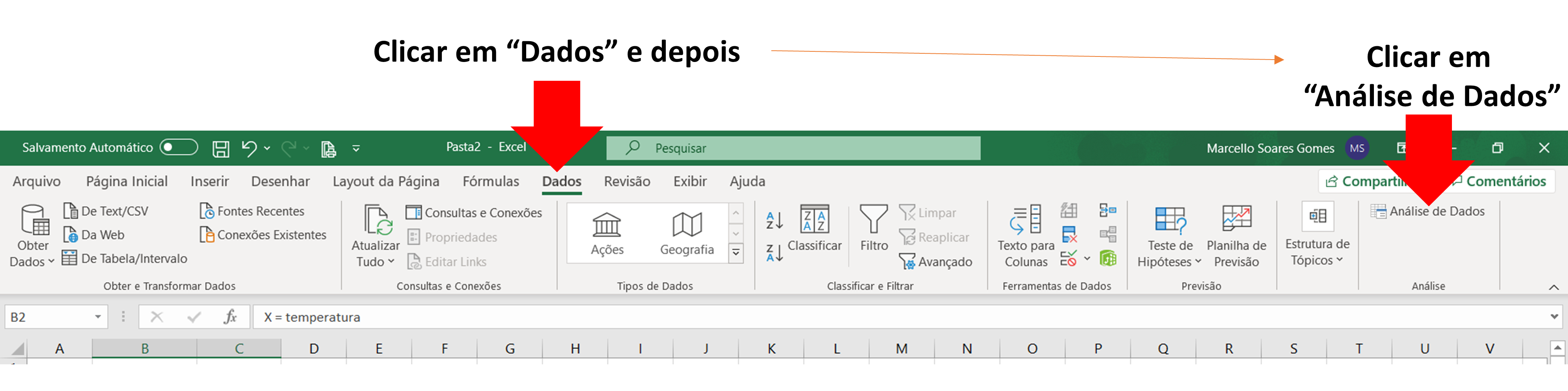
- Clicar em “Dados” e depois em “Análise de Dados” como mostrado abaixo:
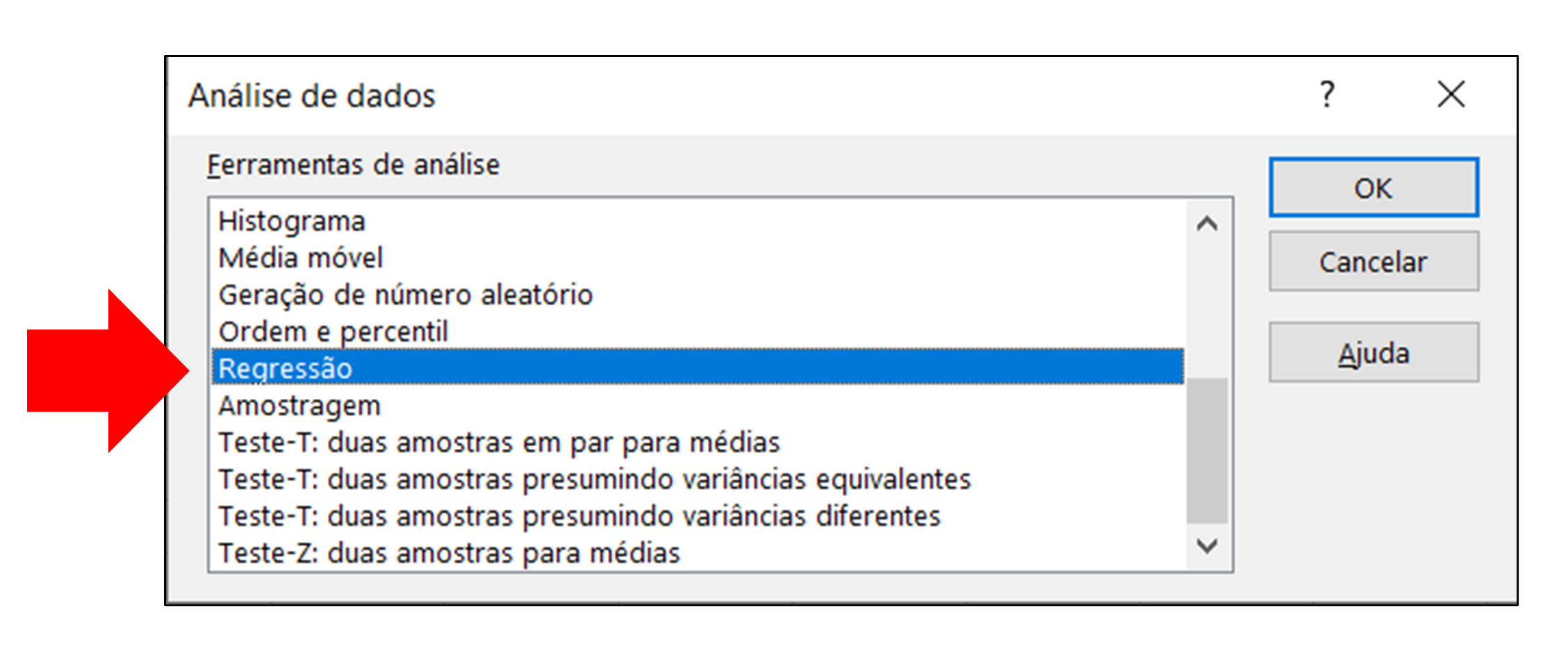
- Clicar em “Regressão” e depois no botão “OK” como mostrado abaixo:
- Preencher a tela da Regressão como mostrado na figura abaixo e depois clicar no botão “OK”:
- Vamos analisar os dados que foram gerados até o momento:
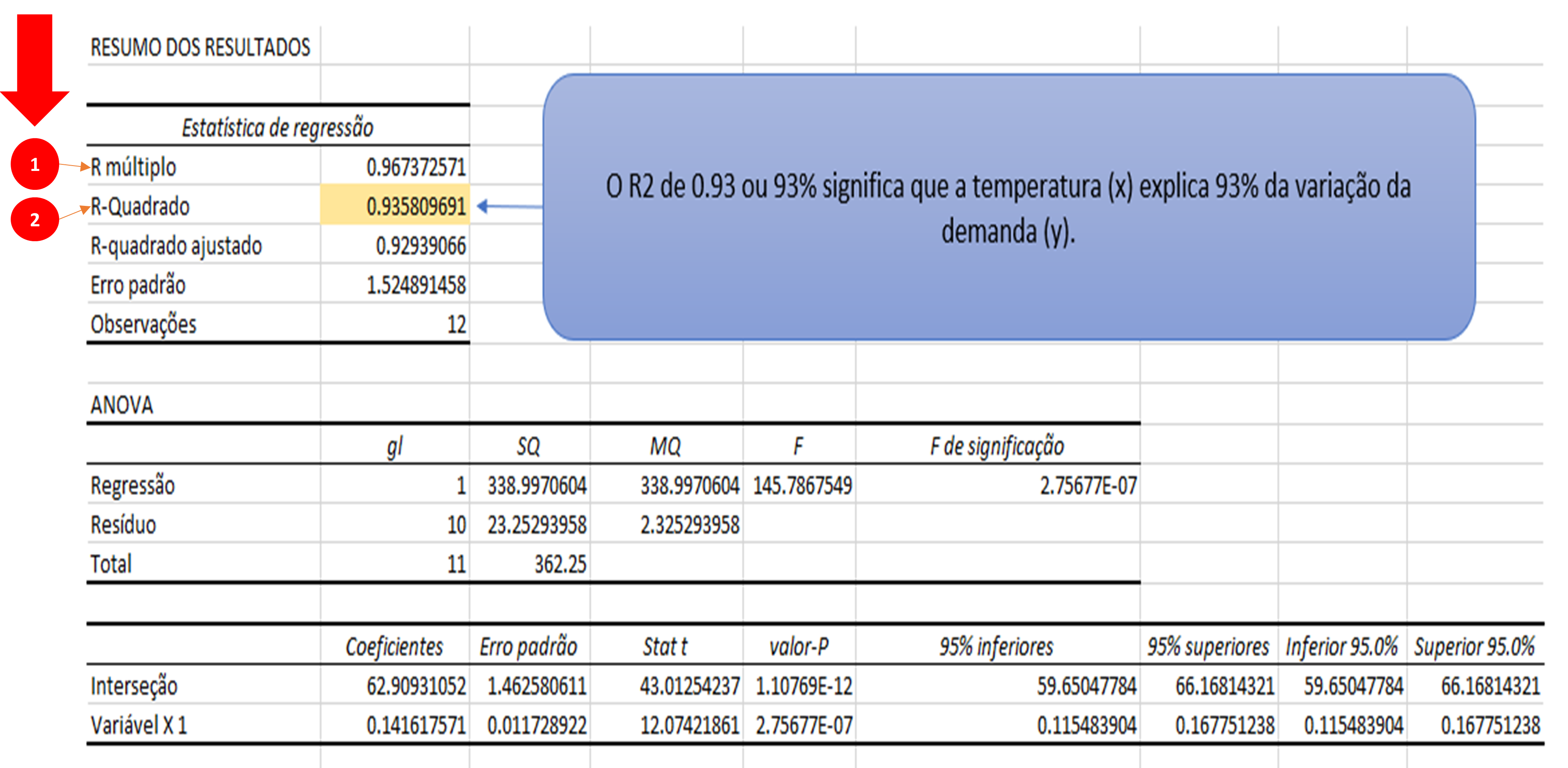
Com base nas informações geradas na figura Regressão Linear abaixo vamos começar a responder as perguntas que foram feitas no início deste artigo.
a) Há influência da temperatura sob a demanda?
A resposta é sim, pois como pode ser visto no item 1 da figura Regressão Linear acima o campo R múltiplo com o valor de 0,967372571 é um valor positivo próximo a 1, o que indica que há influência da temperatura sob a demanda e ele é POSITIVA!
Caso o R múltiplo fosse 0 (zero) significaria que não haveria influência.
Caso o R múltiplo fosse negativo significaria que existiria influência e ela seria negativa, ou seja, se o R múltiplo tivesse dado negativo poderíamos assumir que a temperatura influenciaria negativamente a demanda ou seja, quanto maior a temperatura menor seria a demanda por energia.
b) Se houver influência da temperatura sob a demanda ela é positiva ou negativa?
A resposta é sim, pois como pode ser visto no item 2 da figura acima o campo R múltiplo com o valor de 0,967372571 é um valor positivo próximo a 1, o que indica que há influência da temperatura sob a demanda e ele é POSITIVA!
c) Qual a força da influência da temperatura sob a demanda?
A resposta é que a força é grande, pois se observarmos o item 2 na Figura Regressão Linear acima descrita, o campo R-Quadrado é 0,935809691, que percentualmente equivale dizer que 93,58% da variação da demanda de energia elétrica é explicada pela variação na temperatura (clima)!
O valor ideal procurado numa regressão linear para o R-Quadrado é maior ou igual a 70%.
Ainda resta a pergunta d) Qual a fórmula para prever a demanda de energia elétrica? Para responder vamos continuar com os passos no Excel:
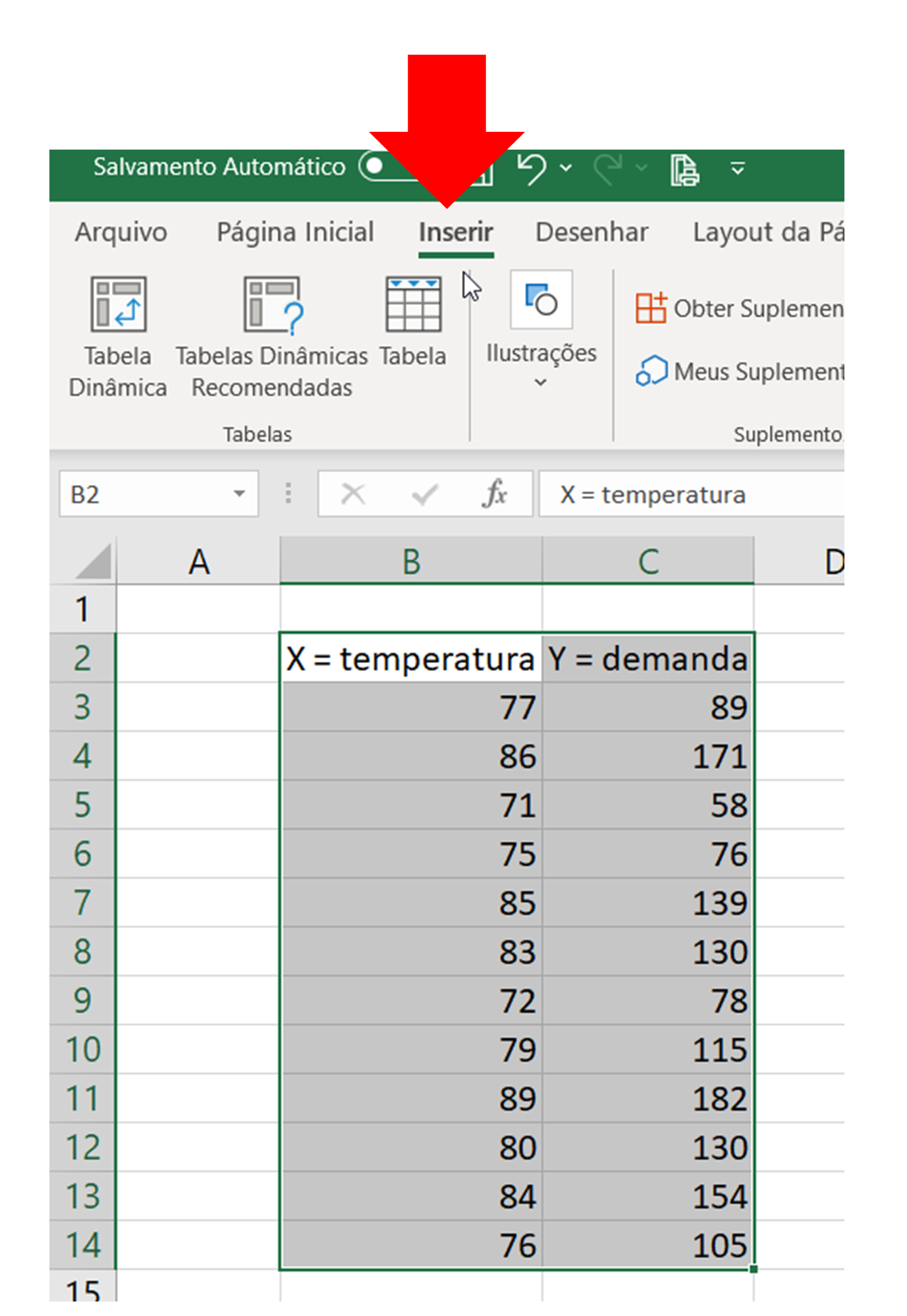
- Selecionar os dados na planilha Excel como mostrado abaixo:
- Clicar na opção “Inserir” do menu do Excel como abaixo:
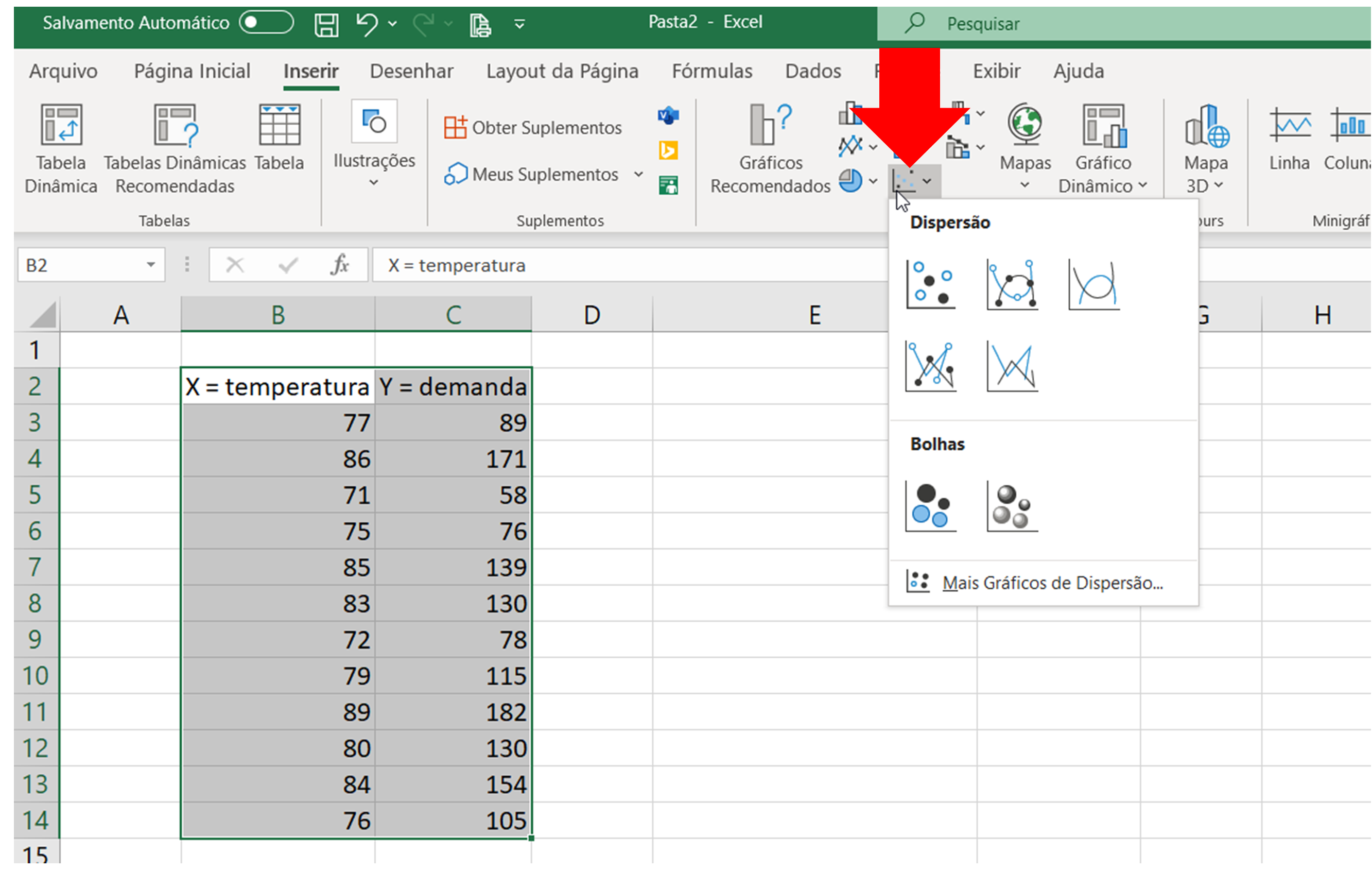
- Clicar na opção “Inserir Gráfico de Dispersão (X,Y) ou de Bolha“, como mostrado abaixo:
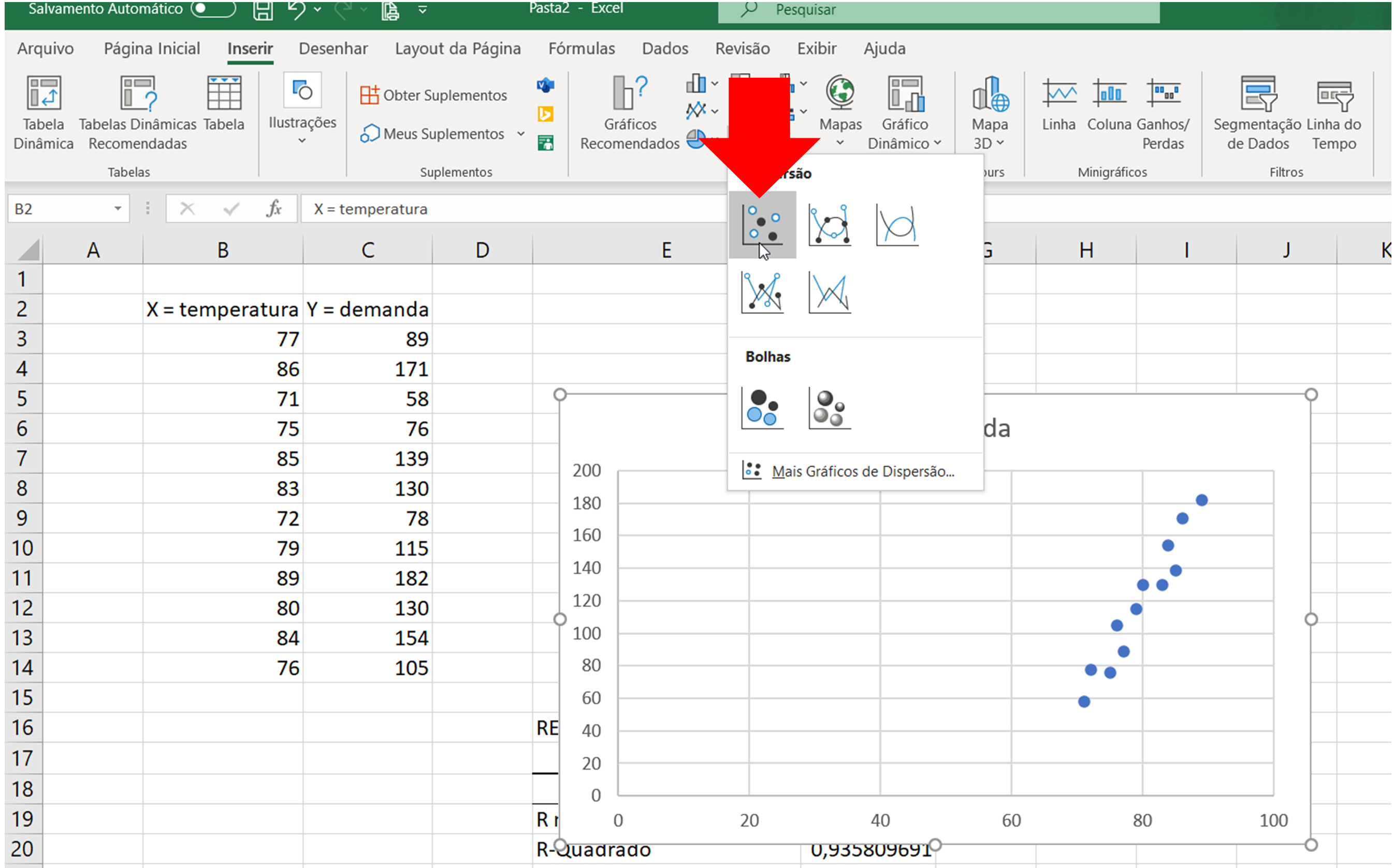
- Clicar na opção de gráfico “Dispersão“, como mostrado abaixo:
- Verificar se gerou o gráfico como o abaixo mostrado:
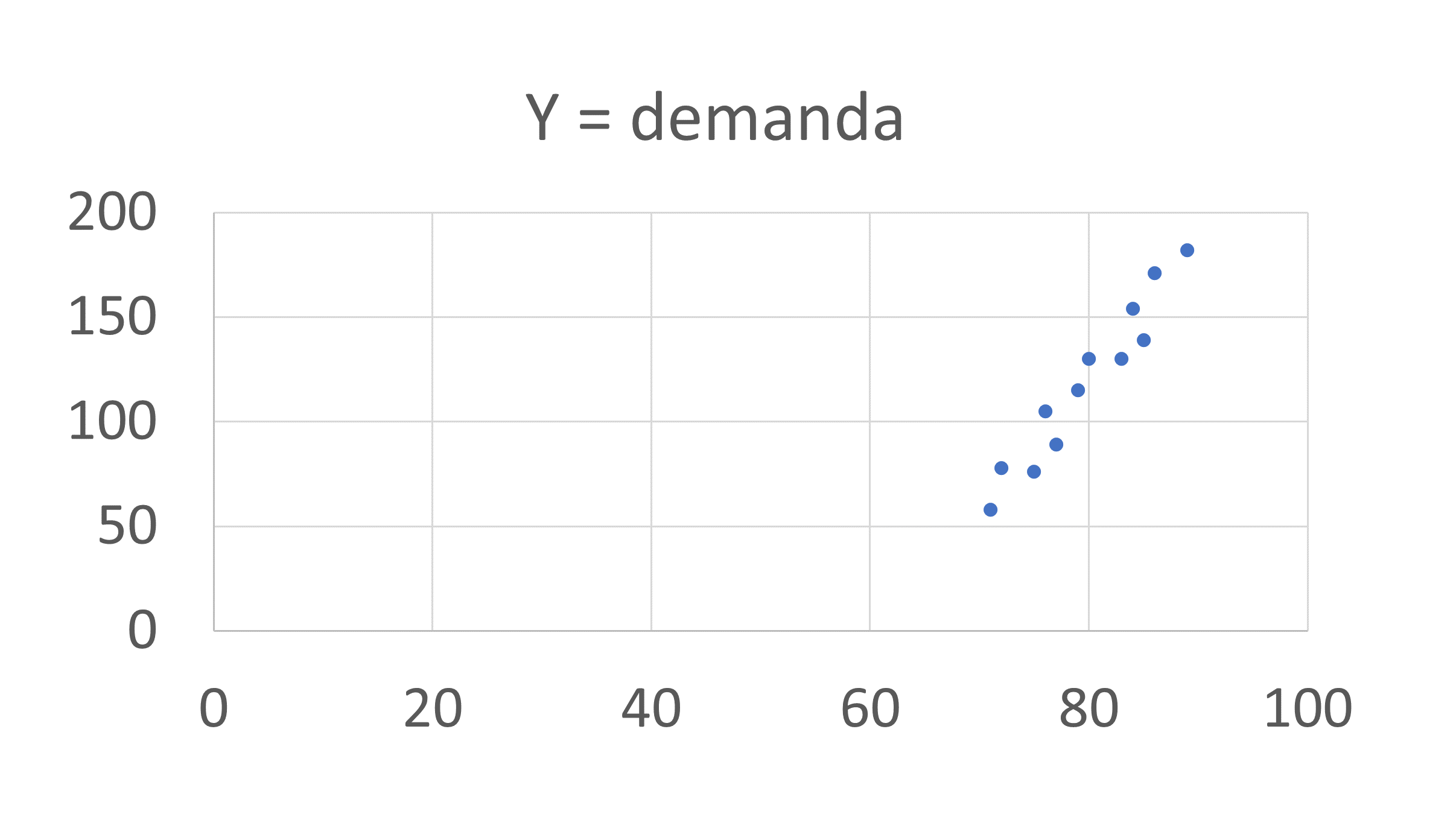
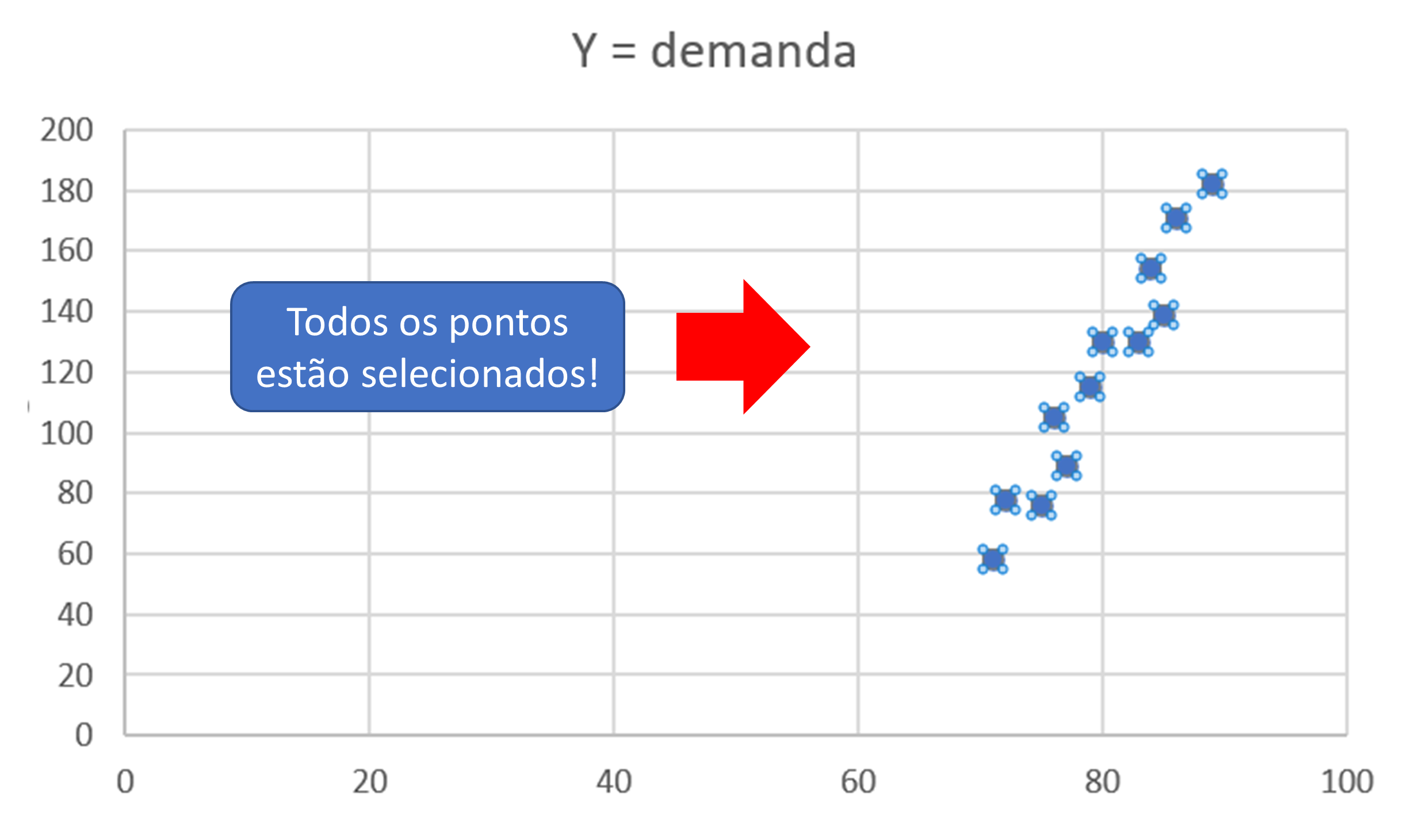
- No gráfico, usando o Excel, selecionar os pontos azuis do gráfico, bastando para isto clicar num dos pontos que o resto é marcado, veja se ficou assim:
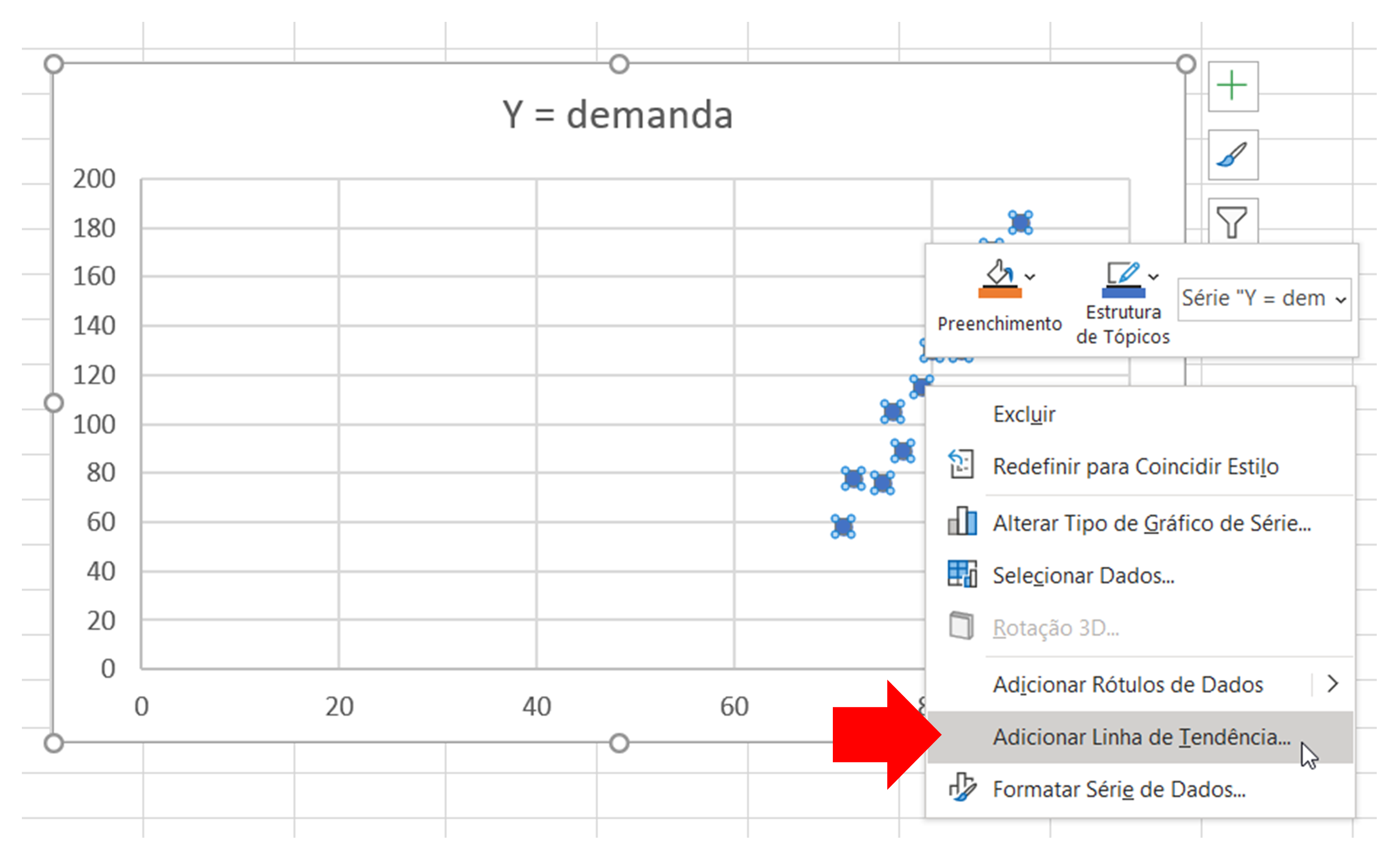
- Com todos os pontos azuis selecionados, clique no botão direito do mouse e selecione a opção “Adicionar Linha de Tendência” como mostrado a seguir:
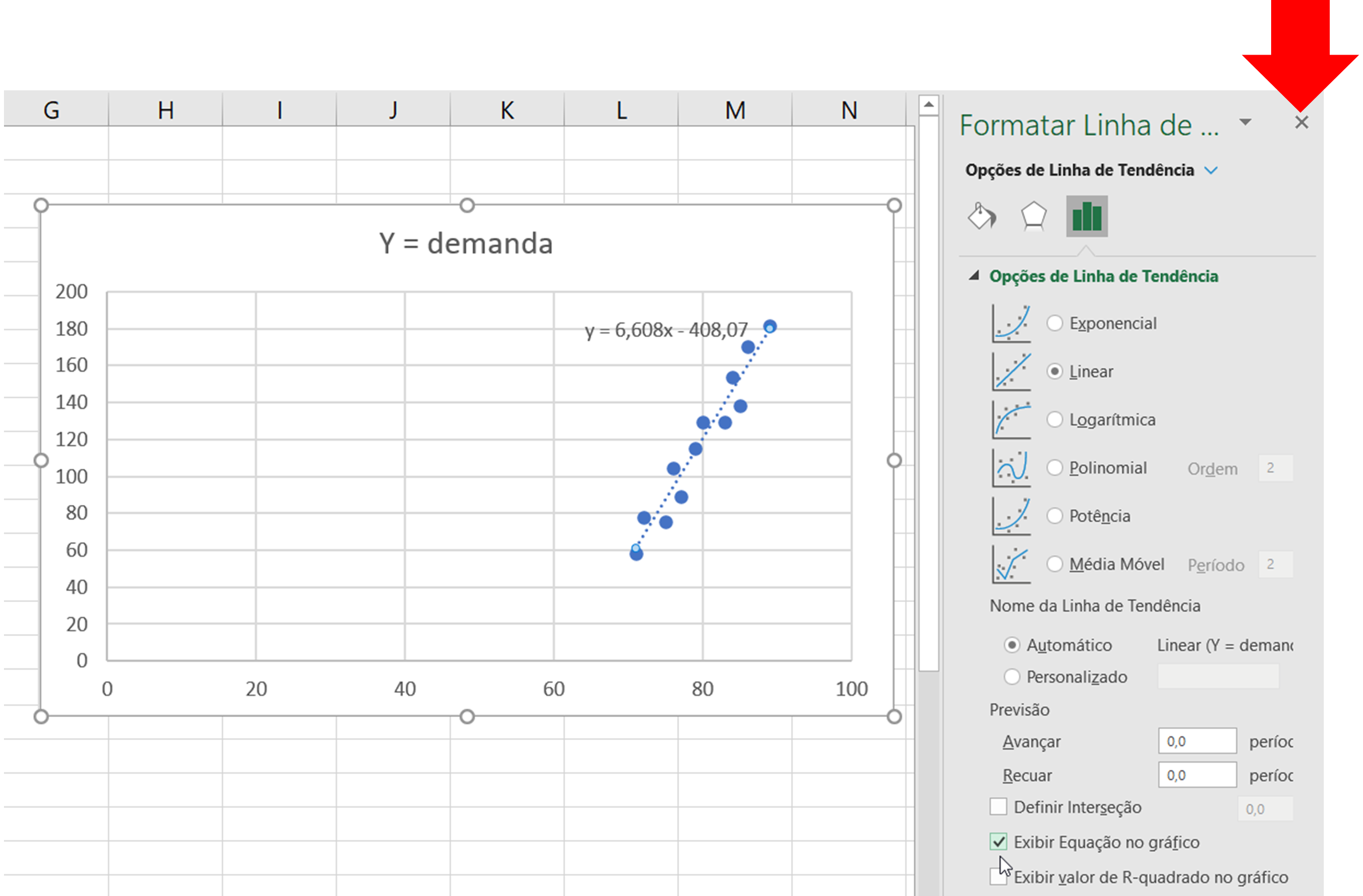
- Marcar a opção “Exibir Equação no Gráfico” como segue:
- Clicar no botão “X” para fechar como se segue:
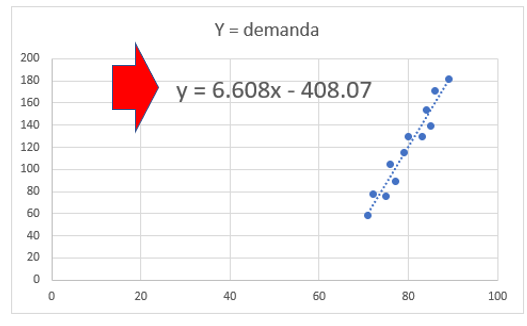
- Veja o resultado final:
A fórmula acima é chamada de “Equação da Regressão” ou “modelo matemático de previsão”, ou seja, com a fórmula acima você consegue fazer a previsão de quanto será o valor da demanda (y) entrando com o valor de temperatura (x).
Bons dados nem sempre contam a história completa. A análise de regressão é comumente usada em empresas para a identificação de causas raízes, pois estabelece que existe uma correlação entre variáveis.
Recomendações:
- Verifique a procedência dos dados de entrada e saída que você usará, pois a regressão não julga se o dado é bom ou não, ou seja, se o dado foi coletado da maneira correta ou se são dados errados;
- Tenha certeza do que você esta analisando, pois neste caso também, a regressão parte do princípio que você sabe o que faz.
- Por exemplo, se você colocar dados de entrada como a velocidade do seu carro, e como valor de saída o valor do dólar, a regressão fará toda a análise, pois ela leva em consideração que você sabe que a entrada e a saída tem alguma relação lógica.
Nosso treinamento Green Belt ensina Regressão Linear e muito mais!
> CONFIRA: o VÍDEO explicando REGRESSÃO NO EXCEL e NO MINITAB, basta clicar em: https://www.laboneconsultoria.com.br/materiais/correlacao/
Caso queira veja também: http://www.stat.yale.edu/Courses/1997-98/101/linreg.htm