Introdução à Análise de Variância
Em estatísticas, a análise de variância (termo muitas vezes abreviado pelo termo em inglês ANOVA) é um conjunto de modelos estatísticos utilizados para verificar se o grupo de meios vêm da mesma população.
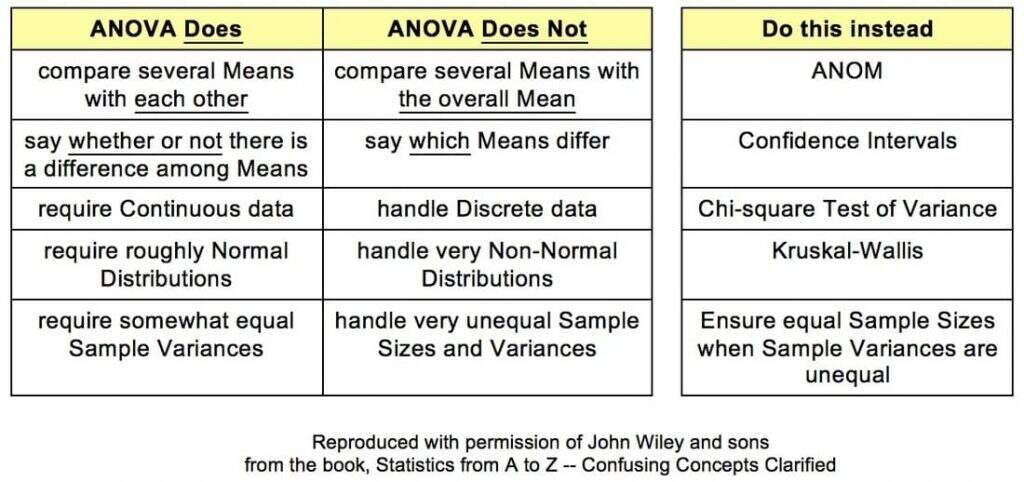
Os grupos correspondem às modalidades de uma variável qualitativa (por exemplo, variável: tratamento; modalidades: programa de treinamento esportivo, suplementos alimentares; placebo) e as médias são calculadas a partir de uma variável contínua (por exemplo, ganho de músculo).
Este teste se aplica quando medimos uma ou mais variáveis explicativas (então chamados fatores de variabilidade, suas diferentes modalidades, por vezes, ser chamado de “níveis”), que têm uma influência sobre a lei de uma variável contínua para ser explicado.
Chamamos de análise de um fator quando a análise se refere a um modelo descrito por um único fator de variabilidade, análise de dois fatores ou análise multifatorial.
Tabela de Conteúdo
- A História da ANOVA
- Suposições básicas
- Hipóteses a serem testadas
- ANOVA unilateral versus ANOVA bidirecional
- Como calcular ANOVA corretamente?
- Exemplo de análise de variância
- Conclusão da ANOVA
A História da ANOVA
O Estatístico britânico Ronald Aylmer Fisher apresenta pela primeira vez o termo variância e propõe sua análise formal em um artigo de 1918 intitulado: “A Correlação entre Parentes na Suposição de Herança Mendeliana”.
No entanto, sua primeira aplicação de análise de variância só foi publicada em 1921.
A análise de variância tornou-se amplamente conhecida depois que foi incluída no livro de Fisher: “Statistical Methods for Research Workers“, de 1925.
O Princípio
A análise de variância permite estudar o comportamento de uma variável quantitativa a ser explicada em função de uma ou mais variáveis qualitativas, também denominadas nominais categóricas.
Quando quisermos estudar o poder explicativo de várias variáveis qualitativas ao mesmo tempo, usaremos uma análise de variância múltipla (MANOVA).
O Modelo
O primeiro passo em uma análise de variância consiste em escrever o modelo teórico de acordo com o problema a ser estudado.
Muitas vezes, é possível escrever vários modelos para o mesmo problema, de acordo com os elementos que se deseja integrar no estudo.
O modelo geral está escrito:
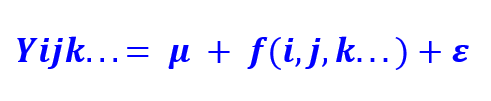
Com Yijk a variável quantitativa a ser explicada, “mi” uma constante, f uma relação entre as variáveis explicativas , e o “e” o erro de medição.
Colocamos a suposição fundamental de que o erro segue uma distribuição normal:
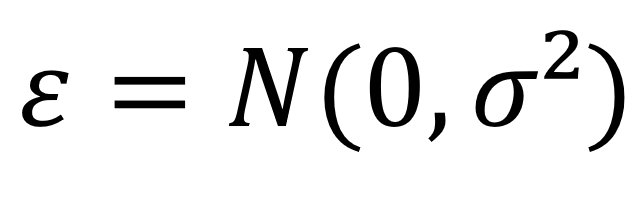
Variáveis explicativas
Existem dois tipos de variáveis categóricas: com ou sem efeito aleatório. Para uma variável com efeito fixo, para cada modalidade, existe um valor fixo correspondente.
Está escrito no modelo teórico com letra maiúscula:
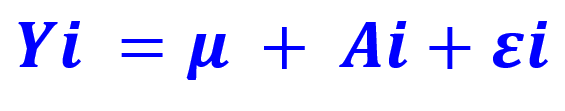
com A0 = A para i = 0, A1 = A para i = 1, etc.
Observe que a variável quantitativa Yi será sempre igual a “mi” acrescido de Ai (apesar de Ai poder assumir valores positivos ou negativos).
No caso de uma variável com efeito aleatório, a variável resulta de uma distribuição normal assumida que é adicionada ao valor fixo.
Eles são escritos no modelo teórico com uma letra grega minúscula:
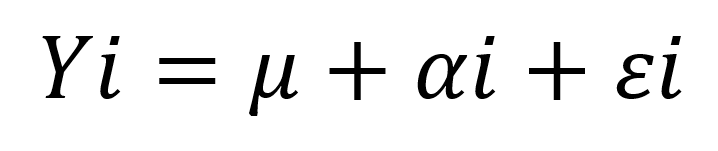
com ai= μa + є∝ e є∝ = N (0, σ²∝ )
Um modelo baseado apenas em variáveis explicativas com efeitos fixos e efeitos aleatórios é denominado modelo misto.
Suposições básicas
A forma geral da análise de variância é baseada no teste de Fisher e, portanto, na normalidade das distribuições e na independência das amostras.
Normalidade da distribuição
Assume-se, na hipótese de nulidade, que as amostras provêm da mesma população e seguem uma distribuição normal.
É necessário, portanto, verificar a normalidade das distribuições e a homocedasticidade (homogeneidade das variâncias, pelos testes de Bartlett e Levene, por exemplo).
Caso contrário, podemos usar as variantes não paramétricas da análise de variância (ANOVA de Kruskal-Wallis ou ANOVA de Friedman).
Independência das amostras
Assume-se que cada amostra analisada é independente das demais amostras.
Na prática, é esse o problema que nos permite supor que as amostras são independentes.
Um exemplo frequente de amostras dependentes é o caso de medições com repetições (cada amostra é analisada várias vezes).
Para amostras dependentes, a análise de variância de medidas repetidas ou ANOVA de Friedman será usada para casos não paramétricos.
Hipóteses a serem testadas
A hipótese nula corresponde ao caso em que as distribuições seguem a mesma distribuição normal.
A hipótese alternativa é que há pelo menos uma distribuição cuja média se desvia das outras médias:
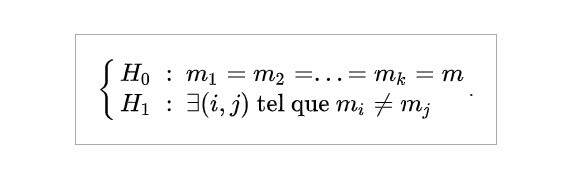
A Fórmula para ANOVA é:
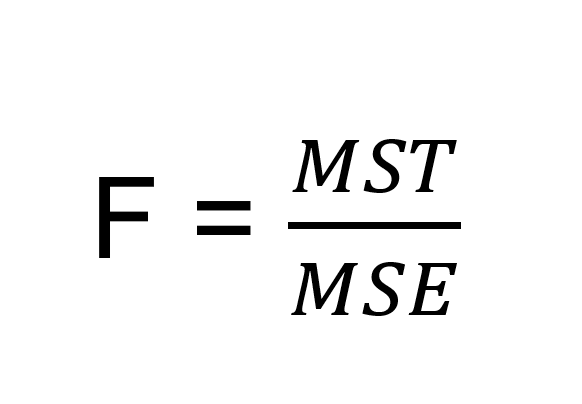
Onde:
F= Coeficiente ANOVA;
MST= Soma média dos quadrados devido ao tratamento;
MSE= Soma média dos quadrados devido ao erro.
O que a análise de variância revela?
O teste ANOVA é a etapa inicial na análise dos fatores que afetam um determinado conjunto de dados.
Assim que o teste é concluído, um analista executa testes adicionais nos fatores metódicos que contribuem de forma mensurável para a inconsistência do conjunto de dados.
O analista utiliza os resultados do teste ANOVA em um teste f para gerar dados adicionais que se alinham com os modelos de regressão propostos.
O teste ANOVA permite a comparação de mais de dois grupos ao mesmo tempo para determinar se existe uma relação entre eles.
O resultado da fórmula ANOVA, a estatística F (também chamada de razão F), permite a análise de vários grupos de dados para determinar a variabilidade entre as amostras e dentro das amostras.
Se não houver diferença real entre os grupos testados, o que é chamado de hipótese nula, o resultado da estatística F da ANOVA será próximo a 1.
A distribuição de todos os valores possíveis da estatística F é a distribuição F.
Este é, na verdade, um grupo de funções de distribuição, com dois números característicos, chamados de graus de liberdade do numerador e graus de liberdade do denominador.
Principais Vantagens
A análise de variância ou ANOVA, é um método estatístico que separa os dados de variância observados em diferentes componentes para uso em testes adicionais.
Uma ANOVA unilateral é usada para três ou mais grupos de dados, para obter informações sobre a relação entre as variáveis dependentes e independentes.
Se não houver variação verdadeira entre os grupos, o resultado F da ANOVA deve ser próximo a 1.
Como usar a ANOVA?
Um pesquisador pode, por exemplo, testar alunos de várias faculdades para ver se os alunos de uma das faculdades superam consistentemente os alunos de outras faculdades.
Em uma aplicação de negócios, um pesquisador de P&D pode testar dois processos diferentes de criação de um produto para ver se um processo é melhor do que o outro em termos de eficiência de custos.
O tipo de teste ANOVA usado depende de vários fatores. É aplicado quando os dados precisam ser experimentais.
A análise de variância é empregada se não houver acesso ao software estatístico, resultando no cálculo ANOVA à mão. É simples de usar e mais adequado para pequenas amostras.
Com muitos projetos experimentais, os tamanhos das amostras devem ser os mesmos para as várias combinações de nível de fator.
ANOVA é útil para testar três ou mais variáveis. É semelhante a vários testes t de duas amostras. No entanto, isso resulta em menos erros do tipo I e é apropriado para uma série de problemas.
ANOVA agrupa diferenças comparando as médias de cada grupo e inclui espalhar a variância em diversas fontes. É empregado com sujeitos, grupos de teste, entre grupos e dentro de grupos.
ANOVA unilateral versus ANOVA bidirecional
Existem dois tipos principais de ANOVA: unidirecional (ou unidirecional) e bidirecional. Também existem variações de ANOVA.
Por exemplo, MANOVA (ANOVA multivariada) difere de ANOVA, pois a primeira testa várias variáveis dependentes simultaneamente, enquanto a última avalia apenas uma variável dependente por vez.
Uma ou duas vias referem-se ao número de variáveis independentes em seu teste de análise de variância.
ANOVA Unilateral
Uma ANOVA unilateral avalia o impacto de um único fator em uma única variável de resposta. Ele determina se todas as amostras são iguais.
A ANOVA unilateral é usada para determinar se há alguma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes (não relacionados).
ANOVA Bidirecional
Uma ANOVA de duas vias é uma extensão da ANOVA de uma via. Com uma via unilateral, você tem uma variável independente afetando uma variável dependente. Com uma ANOVA bidirecional, existem duas independentes.
Por exemplo, uma ANOVA bidirecional permite que uma empresa compare a produtividade do trabalhador com base em duas variáveis independentes, como salário e conjunto de habilidades.
É utilizado para observar a interação entre os dois fatores e testar o efeito de dois fatores ao mesmo tempo.
Como calcular a ANOVA corretamente?
A Análise de Variância pode ser utilizada em praticamente todos os segmentos, mas para ajudar no seu entendimento, vamos usar como exemplos práticos o uso da ANOVA nos negócios de um modo geral.
A Análise de Variância é definida como uma análise do desempenho de um negócio ou processo por meio de variações que envolvem o processo de calcular o valor e isolar a causa das variações entre o custo real e o custo padrão.
A análise de variância ajuda a analisar a diferença entre o custo real e o custo padrão e fornece a chave para o controle de custos que permite à administração corrigir tendências adversas, bem como compreender as áreas de preocupação e melhoria.
Resumindo, a Análise de Variância envolve o cálculo das Variâncias Individuais e a determinação das causas de cada uma dessas variações.
ANOVA: Custo real
Quando o custo real é maior do que o custo padrão, a análise de variância é considerada desfavorável ou adversa, o que é um sinal de ineficiência e, portanto, reduz o lucro do negócio.
Da mesma forma, quando o Custo Real é menor que o Custo Padrão, a Análise de Variância é considerada Favorável e é um sinal de melhoria na eficiência ou pode ser devido ao produto de produção abaixo do padrão ou um padrão incorreto.
No entanto, é pertinente observar aqui que nem todas as variações relatadas por meio da Análise de Variância são controláveis, algumas também são incontroláveis.
ANOVA: Variação incontrolável
Uma variação incontrolável é aquela que não é passível de controle por ação individual ou departamental e é causada por fatores externos, como uma mudança nas condições de mercado, flutuações na demanda e oferta, etc. sobre os quais a empresa não tem nenhum controle e como tal são incontroláveis por natureza.
Variações a explorar
A Análise de Variância pode ser calculada sob cada elemento de custo para o qual os padrões foram estabelecidos e cada uma dessas variações pode ser analisada para determinar as causas e as ações necessárias podem ser tomadas.
Por exemplo, se houver uma variação no custo do material, a empresa poderá analisar as variâncias totais em termos de componentes, para determinar e isolar as causas que dão origem a cada variância.
Aliás, você pode aplicar essa análise estatística a muitas variáveis diferentes que surgem no mundo dos negócios.
Aqui estão alguns dos principais tipos de variações a explorar:
- Variância de mão de obra;
- Variação de vendas;
- Variação de orçamento;
- Variância de material;
- Variância de sobrecarga variável;
- Variância indireta fixa.
Não existe uma fórmula de análise de variância única para todas as investigações e nem um método mágico para calcular ANOVA.
A análise de variância que você realiza dependerá do tipo de variável que você está analisando. Mas, abaixo seguem algumas das principais fórmulas de como calcular ANOVA:
Fórmula de variação de custo de material:
Custo padrão – Custo real = (quantidade padrão x preço padrão) – (quantidade real x preço real)
Fórmula de variância de mão de obra:
Salários padrão – salários reais = (horas padrão x preço padrão) – (horas reais x preço real)
Fórmula de variação indireta fixa:
(Saída real x Taxa padrão) – Sobrecarga fixa real
Fórmula de variação de vendas:
(Qualidade orçada x Preço orçado) – (Qualidade real x Preço real)
Na maioria dos casos, os analistas executam essas fórmulas usando softwares como o Excel.
No entanto, também é possível realizar um teste ANOVA manualmente usando as seguintes etapas:
1 – Encontre a média para cada grupo que você está comparando;
2 – Calcule a média geral ou média dos grupos combinados;
3 – Calcule a variação dentro do grupo ou o desvio de cada pontuação da média do grupo;
4 – Encontre a variação entre os grupos ou o desvio da média de cada grupo em relação à média geral;
5 – Encontre seu F-ratio, ou proporção de variação entre grupos para variação dentro do grupo.
Exemplo de análise de variância
Vamos entender a Análise de Variância com a ajuda de alguns exemplos:
O Custo Padrão do Produto AB fabricado pela Empresa Exemplo 1 é:

As unidades reais produzidas foram de 8.000 unidades e o custo real é o seguinte:

Com base na ilustração acima, vamos fazer a Análise de Variância para cada componente do Custo:
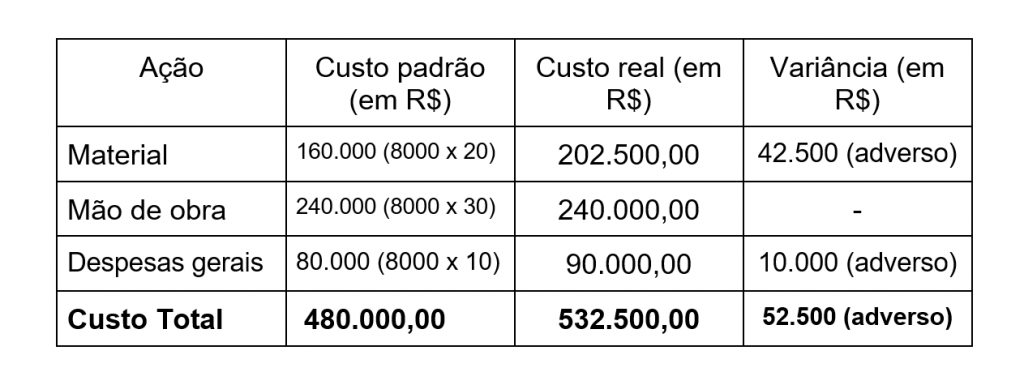
Assim, usando a Análise de Variância, a nossa empresa exemplo pode identificar os componentes de custo que apresentam variação e, portanto, pode tomar ações corretivas.
Conclusão
A análise de variação é uma medida importante na contabilidade de custos e envolve um exame detalhado das variações e sua avaliação, que pode ser baseada no custo ou nas vendas e faz parte integrante do sistema de custo padrão.
Serve como uma ferramenta importante pela qual os gerentes de negócios garantem o controle adequado e realizam ações corretivas sempre que necessário (principalmente no caso de Variação Adversa).
No entanto, deve ser usado nos principais itens de custo e receita para salvaguardar o tempo e o custo envolvidos na realização de tal análise da gestão.