Diagrama de Venn - O que é e como usar essa ferramenta

Diagrama de Venn – Descubra essa ferramenta e suas aplicações

Entender o Diagrama de Venn não é necessariamente algo simples para a maioria das pessoas. O motivo é que se trata de um ramo da matemática que gira em torno da teoria dos conjuntos, algo que envolve figura geométrica e por si só já é um tanto quanto complexo.

O detalhe, porém, é que esse tipo de ferramenta tem sido cada vez mais utilizada em diferentes circunstâncias. Isso inclui, por exemplo, a aplicação em cenários corporativos e de organização de dados.

Diante desse cenário, a compreensão do assunto se torna uma necessidade cada vez maior. Sabendo disso, portanto, buscamos apresentar aqui de maneira simples, uma série de dicas que vão facilitar o entendimento em relação ao assunto. Confira!

O que é o Diagrama de Venn

O termo diagrama em si, pressupõe um modelo visual que simplifica uma ideia ou conceito.

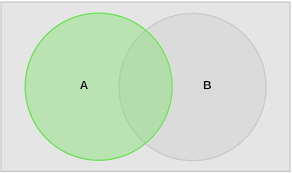
O diagrama de Venn utiliza círculos sobrepostos ou outras formas para ilustrar as conexões lógicas entre algumas coleções de coisas. Muitas vezes, eles são usados para organizar as coisas, enfatizando a maneira como as coisas são diferentes e/ou semelhantes.

Muitas pessoas os encontram na faculdade quando estudam matemática ou lógica, porque os diagramas de Venn tornaram-se parte dos currículos da “nova matemática” dos anos 60.

Estes podem ser diagramas simples entre alguns conjuntos de componentes, ou podem ser muito complexos, como apresentações em 3D, já que avançam para sete ou seis lugares e para fora.

Eles são utilizados para considerar e retratar como as coisas se relacionam com cada um dentro de um determinado “mundo” ou seção. Os diagramas de Venn possibilitam que os usuários visualizem as informações de maneira clara e eficaz e sejam amplamente utilizados em relatórios e apresentações.

Eles estão intimamente ligados aos diagramas de Euler, que variam omitindo conjuntos se não existirem coisas dentro deles. Os diagramas de Venn revelam relacionamentos mesmo quando um lugar está vazio.

No entanto, as origens da forma do diagrama remontam consideravelmente mais longe, pelo menos 600 décadas. A partir de 1200, o filósofo e lógico Ramon Llull (ocasionalmente grafado Lull) de Majorca utilizou um tipo similar de diagrama, escreveu o escritor M.E. Baron em um post de 1969, detalhando sua formação.

Na realidade, John Venn dizia que seus próprios diagramas eram Círculos Euleanos, e não Diagramas Venn.

Exemplo de Diagrama de Venn

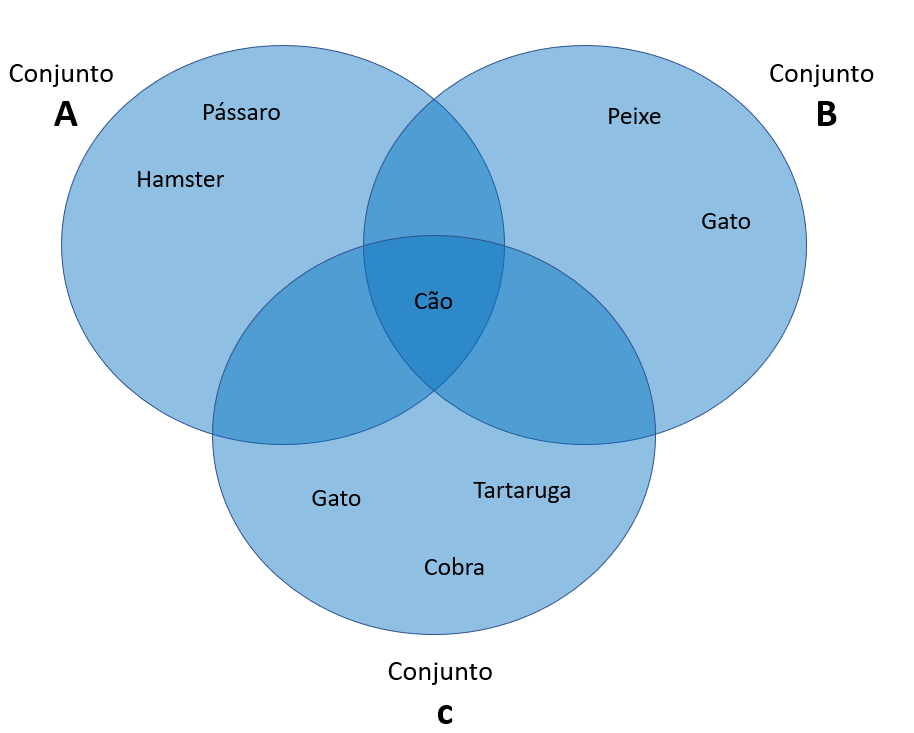
Digamos que nosso mundo é composto por animais de estimação, e gostaríamos de comparar com que tipo de animal de estimação nossos entes queridos concordariam em ter.

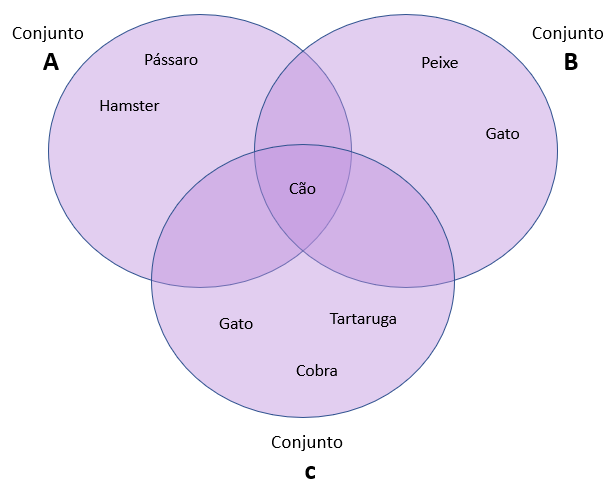
O conjunto A contém meus gostos: pássaro, cachorro, hamster.

O conjunto B compreende os gostos do Membro da Família B: cão, peixe, gato.

O Conjunto C compreende os gostos do Membro da Família C: gato, cachorro, tartaruga, cobra.

A sobreposição, ou junção, desses 3 conjuntos contém cão. Parece que iremos ter um cachorrinho.

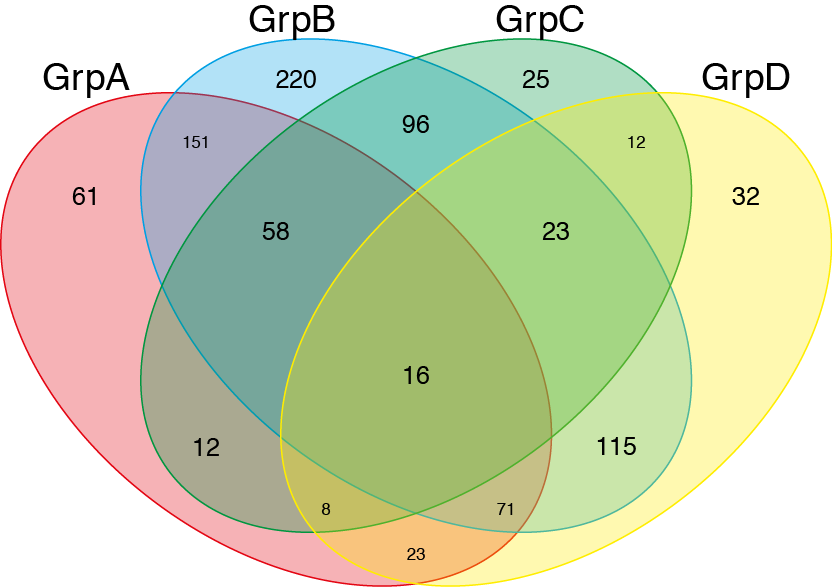
Obviamente, os diagramas de Venn podem ser muito mais desenvolvidos do que isso, já que são amplamente utilizados em vários campos. Veja alguns exemplos:

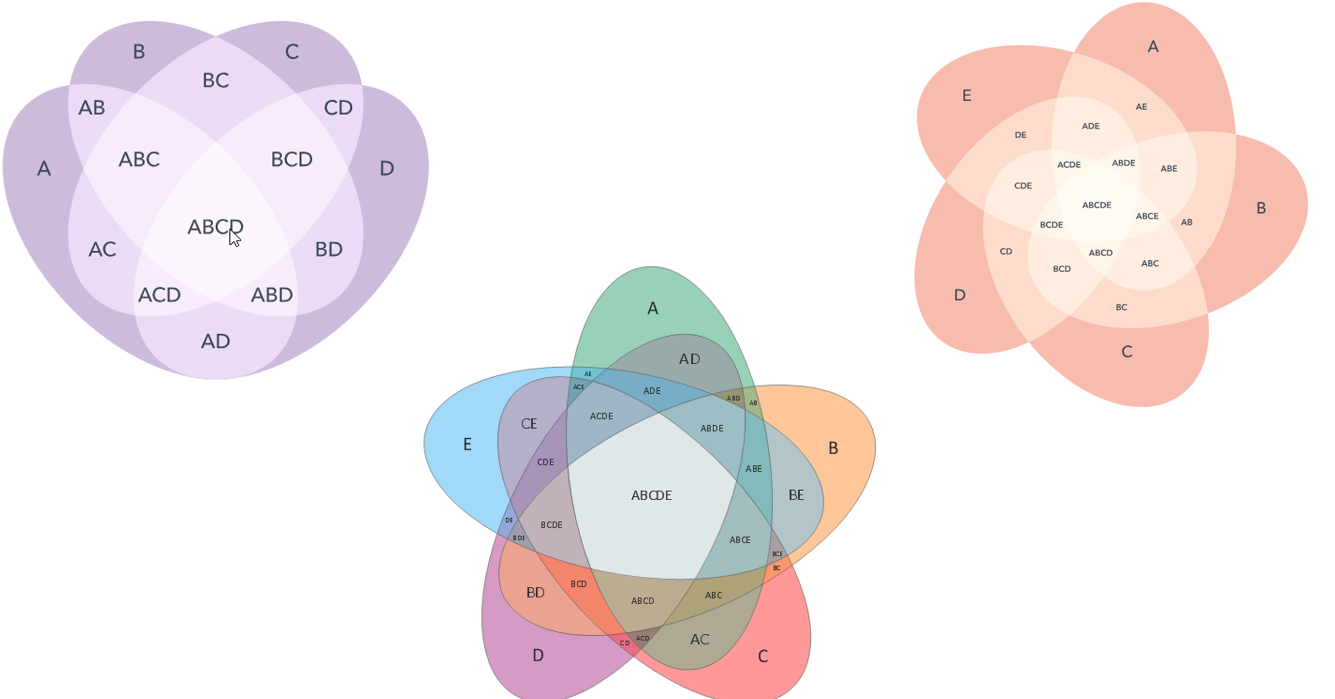
Não por acaso, ele também é utilizado na composição visual de enunciados onde o objetivo é solucionar questões de raciocínio lógico.

Vantagens do Diagrama

Há muitas vantagens no uso desta ferramenta:

Organizar informações para observar a relação entre coleções de itens, como pontos comuns e diferenças.

Estudantes e profissionais podem utilizá-los para considerar a lógica por trás de um conceito, e também para descrever as relações para obter comunicação visual. Este objetivo pode variar de básico a altamente complexo.

Para comparar algumas escolhas e, obviamente, ver o que elas têm em comum versus o que pode distingui-las. Isto pode ser conseguido escolhendo um produto ou serviço importante para comprar.

Para resolver problemas matemáticos complicados. Assumindo que você é um matemático, é claro.

Para comparar conjuntos de dados, encontre correlações e preveja probabilidades de certas ocorrências.

Para concluir através da lógica por trás de equações ou declarações, como a lógica booleana por trás de uma pesquisa de palavras envolvendo declarações “ou” e “e” e a maneira como são agrupadas.

Usos do diagrama de Venn

Matemática: os diagramas de Venn são comumente utilizados na escola para ensinar conceitos básicos de matemática, como conjuntos, uniões e interseções. Eles também são usados em matemática avançada para resolver problemas complexos e têm sido escritos extensivamente em periódicos acadêmicos. A teoria dos conjuntos é um ramo inteiro da matemática.

Estatísticas e probabilidade: os especialistas em estatística usam diagramas de Venn para prever a probabilidade de certas ocorrências. Vários conjuntos de dados podem ser comparados para descobrir níveis de semelhanças e diferenças.

Lógica: Os diagramas de Venn são utilizados para descobrir a validade de argumentos e conclusões específicas. No raciocínio dedutivo, se as premissas são verdadeiras e a forma do argumento é correta, então a conclusão deve ser verdadeira.

Linguística: Os diagramas de Venn são usados para estudar as semelhanças e diferenças entre os idiomas.

E eles são uma ferramenta de comunicação eficaz para ilustrar esse contraste.

Terminologias usadas em Venn

Conjunto:

Uma coleção de coisas. Dada a versatilidade dos diagramas de Venn, as coisas podem realmente ser qualquer coisa. As coisas podem ser chamadas de itens, objetos, membros ou termos semelhantes.

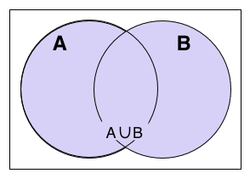
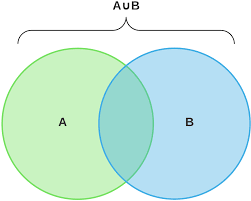
União:Todos os itens nos conjuntos.

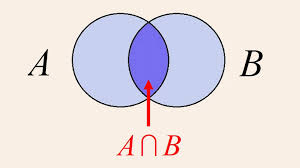
Interseção:

Os itens que se sobrepõem nos conjuntos. Às vezes chamado de subconjunto.

Diferença simétrica de dois conjuntos:

Tudo menos a intersecção.

Complemento absoluto:

O complemento absoluto de A é o conjunto de elementos em U (união), mas não em A.

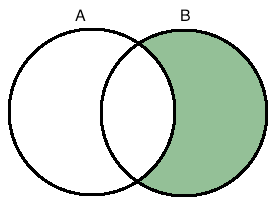
Complemento relativo:

Está em um conjunto, mas não o outro.

Diagrama de Venn escalado:

Também chamado de Área Proporcional. Os círculos (ou outras formas) são dimensionados por sua representação proporcional do todo.

Triângulo de Reuleaux:

Forma formada a partir da interseção de três circulares ou formas, como em um diagrama de Venn.

Definir notações:

Os conceitos ilustrados nos diagramas de Venn são expressos com notações matemáticas, como aquelas que representam conjuntos e subconjuntos (entre parênteses), uniões (com um símbolo semelhante a U) e interseções (com um símbolo U invertido).

Teoria de conjuntos:

O ramo de longa data da matemática que lida com conjuntos.

Softwares para desenhar o Diagrama de Venn

Há opções muito boas para desenhar diagramas de Venn, e dentre as opções seguem alguns nomes:

Conheça mais sobre o Yellow Belt: https://www.laboneconsultoria.com.br/treinamentos/yellow-belt-o-que-e/