O que é e como usar a Distribuição Binomial?
A distribuição binomial está inserida no grupo da distribuição teórica da probabilidade. Afinal, ela ajuda a identificar quais as chances de um resultado específico ocorrer a partir de dados anteriormente verificados.
Sendo assim, a binomial pode apresentar dois resultados: fracasso ou sucesso.

Mas você sabia que a distribuição binomial, além de ser útil na determinação de probabilidades, também pode ser utilizada no ambiente empresarial?
Dentro do ambiente empresarial essa distribuição pode ser utilizada como uma ferramenta de qualificação da gestão.
Ou ainda, em um projeto Six Sigma, para que seja feito um estudo do processo bem como uma estimativa da probabilidade de certo tipo de defeito ocorrer. Sabe o que isso significa?
Que o gestor pode fazer a distribuição da probabilidade para saber quais as chances de sucesso dentro de certa quantidade de provas ou tentativas terá.
Mas qual a importância disso para o gestor? Ao fazer o cálculo das possibilidades que algo pode acontecer, o gestor pode agir de forma preventiva.
Assim, ele evitará que a empresa tenha alguns prejuízos em decorrência de recalls ou trocas, por exemplo.
Isso é totalmente possível com a distribuição binomial já que ela é um dos tipos de distribuição estatística. Sabe o que isso significa?
Qual é a diferença entre distribuição discreta e distribuição contínua? Como calcular a distribuição binomial?
Para conhecer tudo isso e muito mais continue com a gente e veja alguns exemplos de sua aplicação!
Tabela de Conteúdo
- O que é Distribuição binomial?
- Calculando a distribuição binomial
- Quando a distribuição binomial pode ser utilizada?
- Quando uma empresa deve utilizar a distribuição binomial?
- Conclusão da Distribuição Binomial
O que é Distribuição binomial?
A distribuição binomial trata-se de um cálculo estatístico.
Ela é utilizada para determinar a probabilidade de certa ocorrência acontecer dentro de um evento com sistema fechado.
Para isso, é utilizada uma sequência de tentativas limitada.
Na matemática existe uma série de abordagens e de fórmulas que buscam solucionar as questões que envolvem a estatística.
Por esse motivo, não é qualquer distribuição da probabilidade que será considerada binomial. Para isso, algumas características devem ser respeitadas.
A primeira delas é com relação ao espaço amostral. Ele deve ser finito, ou seja, ter fim, ser limitado.
Outra característica é que somente dois resultados podem ser admitidos e por esse motivo essa distribuição recebe o nome de binomial.
Afinal, cada tentativa que for feita com a amostragem será um fracasso ou sucesso. Não há meio termo na distribuição binomial.
Mais uma característica importante dessa distribuição é se todos os elementos pertencentes à amostra possuem as mesmas possibilidades para que a ocorrência seja registrada.
Para finalizar, não deve haver dependência entre os eventos. Ou seja, para que o cálculo retorne um valor que realmente represente a probabilidade os eventos precisam ser independentes.
Assim, as condições normais para aquele conjunto precisam ser levadas em consideração.
Calculando a distribuição binomial
Para fazer o cálculo das possibilidades de certo evento ter determinado sucesso seguindo a distribuição binomial precisamos utilizar uma equação.
Nesse caso, a fórmula que todos utilizam para a determinação da probabilidade binomial é a seguinte:
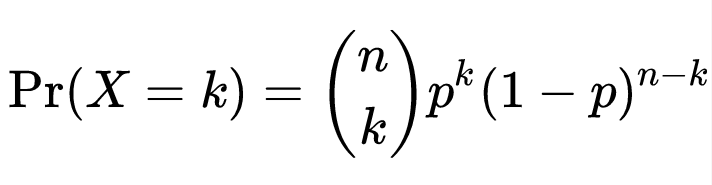
Onde:
- P – probabilidade de sucesso
- (1 – p) ou Q – probabilidade de fracasso
- n – total de ensaios
- k – número de sucessos da amostra
Lembrando que se trata da combinação dos n valores tomados a partir de k até k.
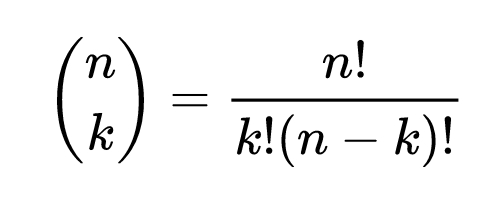
Vamos aprender a calcular essa distribuição utilizando um exemplo? Primeiramente, vamos mostrar o passo a passo de como fazer o cálculo com um exemplo simples.
Depois veremos como a binomial pode ser utilizada dentro da organização. Vamos lá!
Exemplo caixa de ovos
Uma caixa de ovos com 6 unidades possui a probabilidade de 5% de ser quebrado em 3 situações: enquanto é manuseado, no transporte e nas gôndolas.
Qual a probabilidade de na mesma caixa de ovos existirem 2 unidades quebradas?
De acordo com as informações do problema, já sabemos que o total de ensaios n é igual a 6.
Afinal, cada caixa de ovos comporta 6 unidades. Com relação às probabilidades temos duas opções: inteiro ou quebrado.
Para representar a incidência dos ovos quebrados utilizaremos P; para representar a probabilidade de o ovo estar inteiro utilizaremos Q.
Já sabemos, também, que é de 5% a probabilidade de um dos ovos quebrar.
Nesse caso, P é que recebe esse dado. Na porcentagem, temos um número como referencial que é o 100. Assim, para sabermos quais as chances para que um dos ovos quebre é preciso subtrair P de Q.
Assim, teremos:
Q = 100 – P => Q = 100 – 5 => Q = 95.
Ou seja, as chances do ovo não se quebrar, de ficar inteiro, são de 95%. Mas não podemos utilizar esses números em forma de porcentagem na fórmula.
Precisamos transformá-los para que fiquem em forma unitária. Para fazer essa transformação basta dividir a porcentagem por 100.
Dessa forma, transformando 95% na fração 95/100 o resultado fica 0,95.
Caso tenha dúvida se o cálculo está correto basta somar os valores correspondentes a Q e P. Essa soma deve dar 1 como a seguir:
P + Q = 1 => 0,05 + 0,95 = 1 => 1 = 1.
Já temos os valores de P, Q, n, mas e o valor de k? O valor dessa variável é obtido pelo evento que se deseja realizar o cálculo da probabilidade.
No nosso exemplo, queremos saber quais as chances do consumidor adquirir uma caixa com 2 ovos quebrados.
Portanto, o valor de k será 2 que, ao aplicarmos na equação teremos:
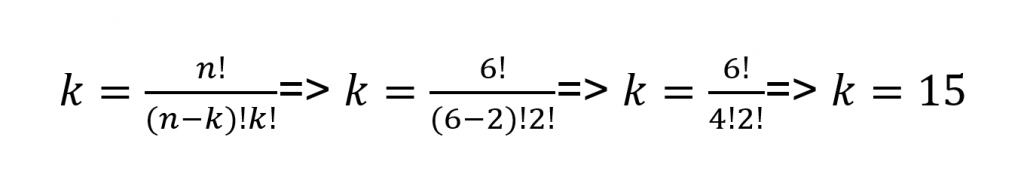
Agora podemos substituir os valores na fórmula da distribuição binomial:
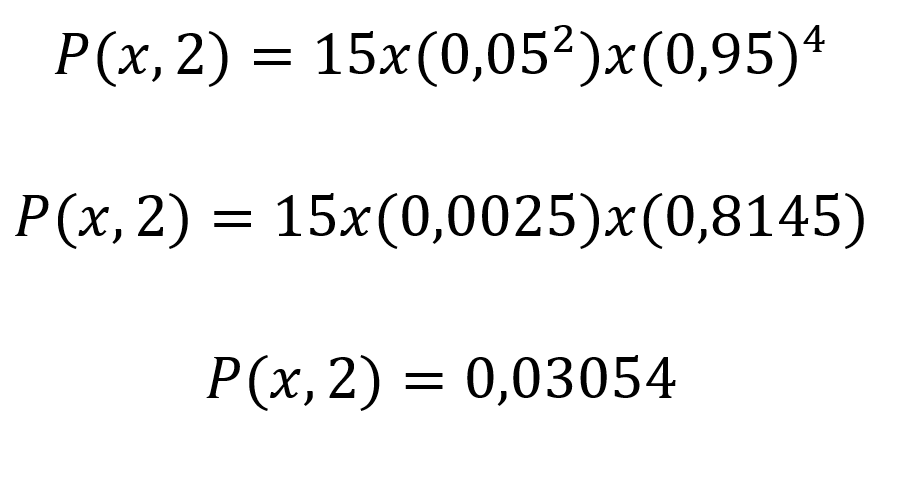
Nesse ponto é preciso converter o valor encontrado para porcentagem e teremos:
P(x,2)=3,054%.
Ou seja, a probabilidade de existir dois ovos quebrados dentro da mesma caixa é de 3,054%.
Exemplo produção de lâmpadas
Em uma fábrica de lâmpadas há uma linha de produção apenas para lâmpadas incandescentes.
O embalamento é feito de forma que 10 unidades das lâmpadas são colocadas em cada embalagem.
O gestor sabe que, dessa linha de produção, a probabilidade de sair uma lâmpada com defeito corresponde a 5%.
O que ele deseja saber é qual a probabilidade de serem embaladas 3 lâmpadas com defeito na mesma embalagem.
Para resolver esse problema precisaremos utilizar a equação binomial:
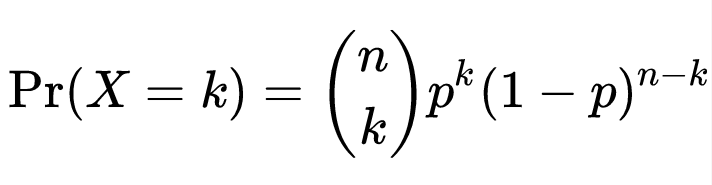
De acordo com o problema apresentado temos os seguintes dados:
- Q = 1 – P = – 0,95;
- P = 0,05;
- n = 10;
- k = 3.
Mas atenção, P não será apresentada a probabilidade de não ser defeituosa a lâmpada, mas a probabilidade de um defeito ocorrer.
Após essa explicação vamos realizar a troca dos valores na equação:
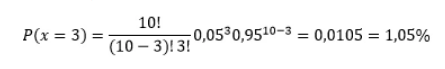
Diante desse resultado o gestor pode concluir que a probabilidade de na mesma caixa serem embaladas 3 lâmpadas com defeito corresponde a 1,05%.
Quando a distribuição binomial pode ser utilizada?
Dentro do ambiente empresarial a distribuição binomial pode ser utilizada quando um projeto Six Sigma for iniciado.
Assim será possível verificar qual tipo de dado está saindo no processo, se contínuo ou discreto.
A partir daí é feita a determinação das ferramentas que terão uso ao desenvolver o projeto.
O profissional deve fazer a definição de qual distribuição estatística consegue representar melhor o processo em estudo.
Já sabemos que existem dois grupos de distribuição estatística: Distribuição Contínua (Variável) e Distribuição Discreta (Atributos).
A distribuição discreta é utilizada quando a saída de interesse somente pode ter valores inteiros.
Por exemplo, falha ou sucesso representados por 0 e 1, quantidade de caras ou coroas. Esse tipo de distribuição divide-se em: Distribuição Poisson e Distribuição Binomial.
Distribuição de Poisson
Siméon Denis Poisson foi um físico e matemático francês que viveu entre 1781 e 1840. Foi ele quem descobriu a distribuição de Poisson.
Enquanto na binomial há um número de provas discreto, em Poisson, o número de sucesso será encontrado dentro de um intervalo contínuo em observação.
Que intervalo será esse? Isso quem vai escolher é a própria pessoa, afinal, pode ser a área de um terreno, certo período de tempo, o comprimento que uma peça de roupa possui entre tantos outros.
Certamente você já obteve um dado importante que foi calculado com a distribuição de Poisson e não percebeu. Vamos ver?
Quantas vezes você viu uma reportagem na TV falando que dentro de determinado período de tempo ocorreram tantos acidentes de trânsito?
Já reparou que no exame de sangue contém a informação que determinada quantidade de glóbulos vermelhos foram visualizadas no microscópio em certa unidade de área?
Esses são alguns exemplos bem práticos e do dia a dia de onde vemos a distribuição de Poisson.
Quando uma empresa deve utilizar a distribuição binomial?
Dentro de uma empresa existem os mais variados tipos de dados que mostram como ela se encontra em diferentes aspectos.
Na gestão, é preciso identificar qual tipo de dado se está lidando para poder determinar o que será analisado.
Já vimos que a distribuição pode ser discreta ou contínua. A primeira possui um número finito de valores e contável como, por exemplo, uma bandeja de ovos e um lote com produtos de higiene.
Quanto a contínua não possui um número exato, pois sua resposta é dada num conjunto de valores.
A distribuição binomial busca valores exatos, ou seja, ela vai determinar qual a probabilidade para que uma determinada ocorrência de eventos aconteça.
Por isso, no ambiente organizacional, ela deve ser utilizada para calcular um número específico que um lote pode apresentar de erros, por exemplo.
Ou seja, ela se mostra muito útil dentro de um sistema fechado, finito, cuja quantidade é determinada.
Entretanto, ela não será útil para determinar a probabilidade de variação no padrão de um produto ou serviço como, por exemplo, dimensão e cor.
Resumindo, quando o gestor possui lotes grandes ou produções contínuas, pode utilizar a distribuição binomial sem qualquer tipo de problema ou receio.
Afinal, ela se mostra muito útil nesse tipo de situação entre outras.
Benefícios da distribuição binomial
Por ser uma forma de determinar uma probabilidade a distribuição binomial já se mostra de grande importância dentro da matemática.
Mas ela também pode, e deve, ser utilizada pelo gestor no dia a dia dos negócios.
Ao fazer isso é possível observar uma série de benefícios que são de grande importância para a empresa.

Principais benefícios para a empresa
Um dos principais benefícios que a binomial oferece às empresas diz respeito à estratégia da produção.
Nesse sentido, a distribuição tem o objetivo de garantir os bons resultados.
Ela se destaca ainda mais na administração por ser capaz de oferecer algo de grande importância: vantagem competitiva a quem se compromete em aplicá-la e utilizá-la de forma inteligente.
A distribuição binomial também pode ser utilizada dentro da fase de planejamento no intuito de realizar estudos preliminares.
Através deles serão indicadas quais as chances para que o erro aconteça. Isso vai permitir que os insumos materiais e os recursos humanos sejam preparados levando em consideração essa previsão e o orçamento.
Mais um benefício que pode ser observado diz respeito ao trabalho executado.
Conclusão da Distribuição Binomial
Quando cálculos estatísticos são realizados eles dão mais segurança ao gestor para que tome as melhores decisões.
Como isso é possível? Simplesmente porque a binomial é capaz de calcular as chances de erro que decorrem de determinada ação.
Assim o gestor passa a ter mais segurança na hora de escolher qual caminho seguir, pois já possui uma ideia mais fiel dos resultados possíveis.
Toda probabilidade é uma estatística e por esse motivo nenhum resultado obtido trata-se de sentença imutável.
Mas a precisão que ela apresenta quando dados reais de uma empresa são utilizados mostram o quão poderosa esse cálculo matemático é dentro da organização.
Afinal, ela consegue fazer a previsão da incidência de erros que estão presentes na produção. Seus resultados servem como base para que ações preventivas sejam tomadas.
Qual a melhor forma de evitar dores de cabeça dentro de uma organização e prejuízos financeiros que ocorrem por causa de recalls, trocas e devoluções?
Fazendo a antecipação dos erros que podem surgir. Isso a distribuição binomial é capaz de fazer com grande maestria.