Introdução à Distribuição de Poisson
A distribuição de Poisson é mais um dos tipos de distribuição estatística existentes e que pode ser utilizada nas mais variadas ocasiões e objetivos.
Tabela de Conteúdo
- O que são distribuições de probabilidade?
- Tipos de Distribuições de Probabilidades
- Fórmula de Poisson
- Conclusão da Distribuição de Poisson
O que são distribuições de probabilidade?
Quem nunca estudou algum assunto de matemática e ao terminar os estudos sentiu que nunca utilizou aquele conhecimento? Um ótimo exemplo é a fórmula de Báskara.
Outro exemplo neste sentido é a distribuição de Poisson. Mas, afinal, como ela pode ser útil no trabalho ou no dia a dia?
Primeiramente, lembre-se que Poisson trata-se de uma estatística, uma forma de determinar a probabilidade de algo acontecer.
Quando se prevê algo fica muito mais fácil tomar uma decisão quanto ao que fazer, o que não fazer, qual caminho seguir. Ou seja, Poisson vai ajudar a tomar decisões, principalmente no ambiente organizacional.
A importância das probabilidades na tomada de decisões
A tomada de decisão não é algo tão simples de ser feito já que envolve muitos aspectos e interesses. Para que esse momento se torne mais sensato e menos difícil é fundamental analisar alguns dados importantes.
Até mesmo alguns cálculos devem ser feitos com o intuito de obter uma estimativa mais próxima da realidade.
As distribuições de probabilidade ou lei de probabilidade como também são conhecidas ajudam na tomada de decisão.
Elas são muito úteis quando são adotados uma modelagem e até mesmo problemas que exijam uma conclusão tendo como princípio uma amostra coletada.
Observações importantes
Como saber qual tipo de distribuição deve ser utilizada? Para isso, é preciso verificar a natureza da variável que está passando pela análise.
Também é preciso ter ferramentas que ajudem a definir a distribuição que será utilizada tendo como base as informações que foram extraídas da amostra.
É importante conhecer um pouco da distribuição binomial para diferenciá-la e compreender melhor quando deve ser utilizada.
Seu intuito é determinar quais as chances de determinado evento ocorrer dentro de um intervalo que pode ser de tempo, de volume, de área, por exemplo.
Este é um assunto que comumente é abordado dentro da matemática, mas o que poucos sabem é onde aplicá-lo.
Uso nos negócios
Nas organizações que utilizam o método DMAIC, por exemplo, o cálculo de Poisson se mostra de grande importância para medi-lo. Afinal, não é difícil fazer sua interpretação.
Mas não acredite que exista apenas esse tipo de distribuição estatística, pois a distribuição de Poisson é apenas uma dentre outras.
Quer um exemplo de outro tipo de distribuição estatística que existe e que também é muito utilizada nas organizações? A distribuição binomial é um desses tipos de probabilidade.
É claro que um bom gestor deve dominar essa e outras técnicas de probabilidades, afinal, todo negócio possui dados de suma importância que devem ser muito bem examinados e calculados da forma correta.
São esses dados que vão mostrar ao administrador qual a melhor decisão a ser tomada naquele momento junto com outras análises.
Que tal compreendermos melhor o que é a distribuição Poisson, aprender a calculá-la, ver alguns exemplos e saber a importância dela para a organização?
Tipos de Distribuições de Probabilidades
As distribuições se dividem em alguns tipos como a distribuição binomial e a de Poisson, por exemplo. Definir qual deve ser utilizada é essencial para obter resultados mais fidedignos.
Para ter essas informações, vejamos mais detalhes!
A distribuição binomial
Dentro da estatística, a distribuição binomial é muito utilizada e não poderia ser diferente já que ela é uma metodologia quantitativa.
Através dela, é possível determinar a probabilidade em cenários variados. No ambiente empresarial ela também é muito utilizada e funciona muito bem com ferramentas que qualificam a gestão.
Para que a binomial seja utilizada algumas características devem estar presentes como:
- Espaço amostral finito;
- Possibilidades iguais para que todos os elementos da amostra sejam registrados;
- Os eventos não podem depender uns dos outros para que haja a representação da probabilidade.
Dessa forma, esse tipo de distribuição estatística é capaz de retornar dois resultados que são: sucesso e fracasso.
Agora que já sabemos um pouco da distribuição binomial, que tal conhecermos as características da distribuição de Poisson?
A Distribuição de Poisson
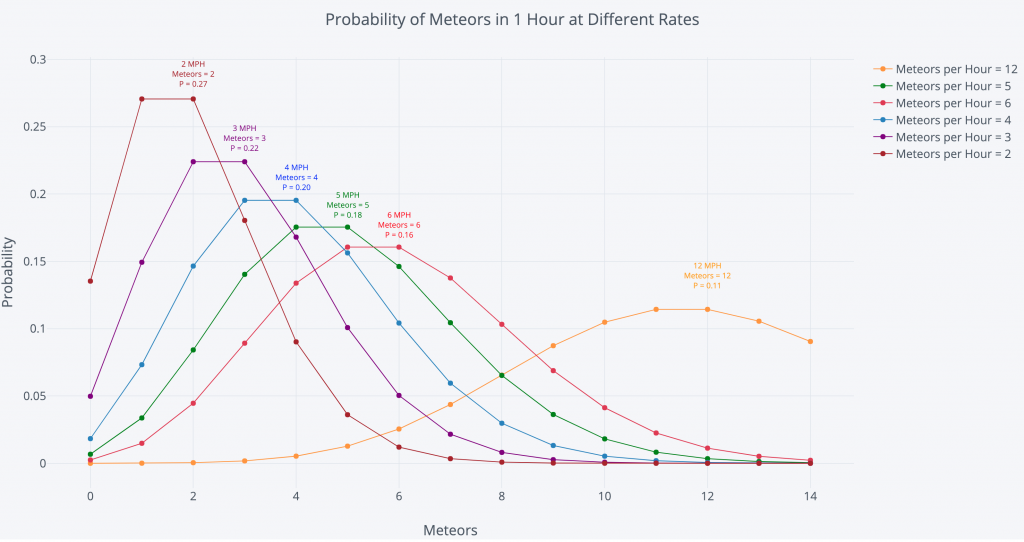
Na matemática o que não faltam são fórmulas para determinar os mais variados itens. Encontrar a área de figuras geométricas, determinar as chances de algo acontecer são apenas algumas delas.
A distribuição de Poisson também se trata de um método matemático que é bastante utilizado nos mais variados segmentos.
Ela vai determinar qual a probabilidade de certa ocorrência discreta ocorrer. Mas para isso, é importante que alguns parâmetros sejam observados, caso contrário, outra fórmula de probabilidade deve ser utilizada.
No caso de Poisson, sua aplicação ocorre quando a quantidade de ocorrências possíveis são muito superiores ao número médio das ocorrências.
Essa maioria deve ser levada em consideração quando analisada dentro de um espaço ou intervalo de tempo. Mas atenção, é comum não saber a quantidade dessas ocorrências possíveis.
Como fazer para reconhecer a distribuição de Poisson?
Para isso, é preciso observar se três aspectos estão presentes:
1 – Irá calcular a quantidade de vezes que determinado evento ocorre em certo período que pode ser de tempo, volume, área entre outros;
2 – As chances de ocorrer o evento não muda em cada intervalo, ou seja, ela se mantém a mesma em todos os intervalos;
3 – O número das ocorrências presente em um intervalo não é dependente de outro.
Exemplos de sua aplicação
Para que fique bem mais claro quando que Poisson pode ser utilizado vamos ver alguns exemplos de sua aplicação:
- Acidentes envolvendo automóveis em uma estrada;
- Números de carros que chegam ao posto de gasolina;
- Número de requisições que um servidor recebe dentro de um intervalo de tempo;
- Quantidade de clientes que passam no caixa do supermercado;
- Erros de digitação que ocorrem em determinado período de tempo.
Já sabemos o que é, os critérios para sua utilização e até alguns exemplos de onde se aplica a distribuição de Poisson. Só está faltando aprender a calcular e é o que vamos fazer a seguir:
Fórmula de Poisson
Para que a distribuição de Poisson possa chegar a um resultado é preciso utilizar sua fórmula. Com ela, é possível determinar a probabilidade. Assim, sua fórmula é a seguinte:
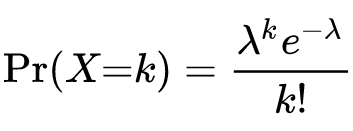
Para essa equação e sua correta utilização devemos considerar o seguinte das suas variações:
- Lâmbda – número real que corresponde ao número de ocorrências que se espera dentro de um determinado intervalo de tempo
- Pr – tende ao valor;
- x – é uma variável aleatória que terá o valor k;
- k – número inteiro que não pode ser negativo, pois corresponde a quantidade de vezes que, dentro de certo intervalo, um evento ocorre;
- e – trata-se do número de Euler que é irracional e cujo valor aproximado é 2,71828.
Como encontrar o valor do lambda?
Imagine que o tempo de ocorrência de um evento tem média de 5 minutos. O que queremos é determinar a quantidade de eventos que terão ocorrência dentro do intervalo de 15 minutos.
Para determinar o valor do lambda que usamos na distribuição de Poisson teremos que calcular seu valor da seguinte forma:
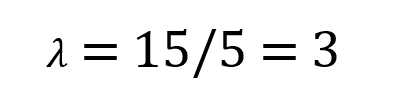
Ou seja, dentro da fórmula de distribuição de Poisson, o valor que colocaríamos para o lambda seria 3.
Agora vamos ver alguns exemplos de aplicação dessa equação e aprender a calculá-la?
Exemplo aplicado a banco
Suponhamos que um banco realizou a coleta de dados e a partir daí percebeu-se que em uma hora, 6 clientes adquirem certo seguro.
Agora, a instituição deseja saber qual a probabilidade de, no mesmo período de tempo, 8 seguros serem vendidos.
De acordo com os dados que possuímos percebemos que as três características que são necessárias para fazer o cálculo da distribuição de Poisson estão presentes.
Assim, temos que o valor de é igual a 6 já que esta é a média da distribuição e o k é igual a 8, pois essa é a quantidade de vezes que se deseja considerar para a ocorrência.
O valor de Euler é um número fixo que corresponde a 2,71828.
Assim, ao realizarmos a troca dos valores na equação teremos:
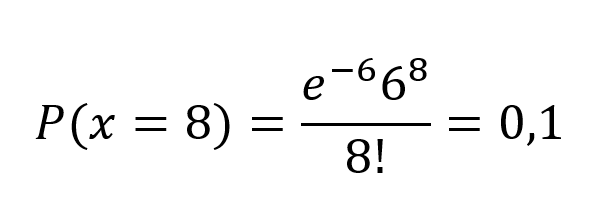
Mas o que essa resposta, 0,1, significa? Quer dizer que a probabilidade de 8 seguros serem vendidos no período de uma hora corresponde a 10%.
Vamos ver mais um exemplo para compreendermos ainda mais como Poisson é calculado?
Exemplo aplicado a corretor de seguro
Em uma semana, um corretor de seguro de vida consegue realizar, em média, 3 vendas desse produto.
Utilizando a distribuição de Poisson deseja-se saber quanto que em uma certa semana ele consegue vender alguns seguros.
Conforme o enunciado, y= 3. Afinal, alguns seguros significa que são 1 ou mais.
Assim, teremos:
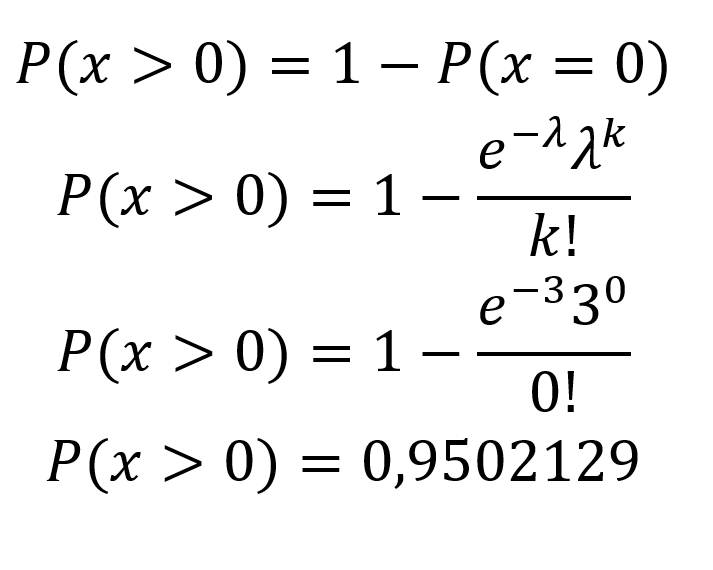
Exemplo aplicado a trânsito
Durante o verão há uma intersecção que registra 2.00 de colisões, em média, dentro de uma semana.
Assumindo que os pressupostos de Poisson são todos satisfeitos, é preciso determinar a probabilidade de não ocorrer colisão nessa intersecção em certa semana.
Para realizar o cálculo temos os seguintes dados:
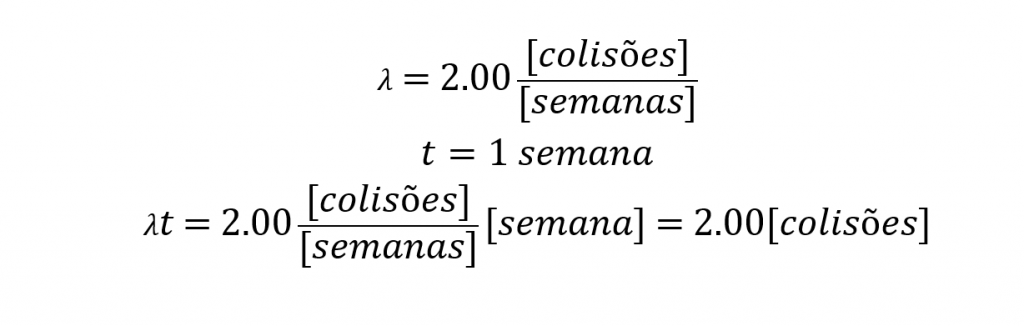
Agora, vamos realizar o cálculo da probabilidade:
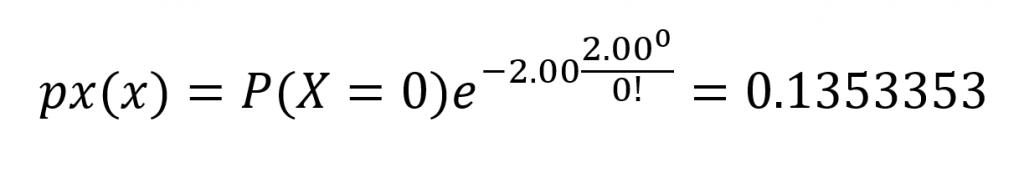
A partir desse exemplo, se quiséssemos calcular a probabilidade de haver apenas uma colisão em determinada semana o cálculo seria realizado da seguinte forma:
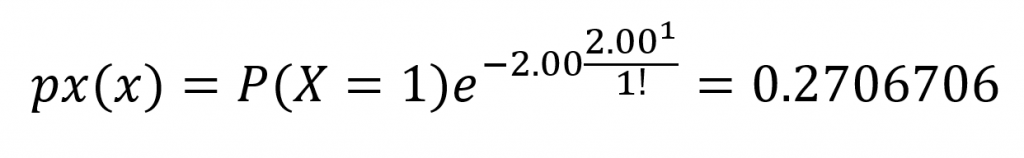
E se quiséssemos determinar a probabilidade de em certa semana ocorrerem duas colisões nessa interseção?
O cálculo seria feito da seguinte forma:
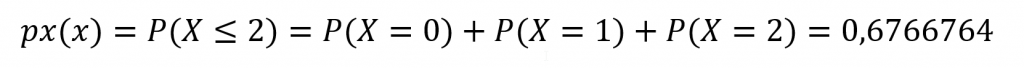
Para saber a probabilidade de não ocorrer um número de colisões maior que dois na semana o cálculo é um pouco diferente.
Fica assim:
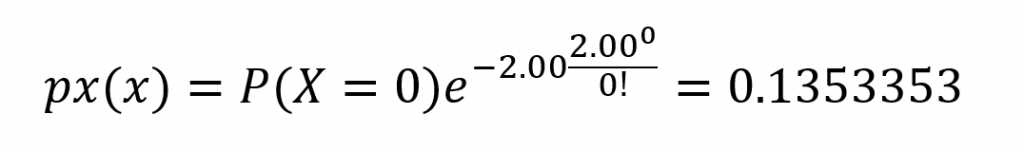
Agora, se quisermos encontrar a probabilidade de ocorrer mais que duas colisões na mesma semana o cálculo seria realizado assim:
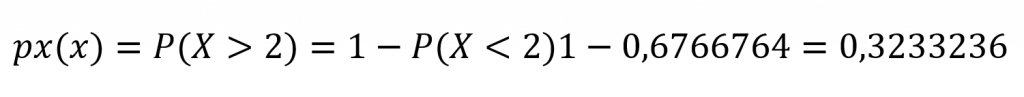
Conseguiu compreender como o cálculo de Poisson é feito? Que tal vermos quando esse tipo de distribuição de probabilidade pode ser utilizado?
Quando aplicar a distribuição de Poisson?

Quando se fala na produção de um produto é natural que a organização tenha atenção para que erros sejam reduzidos ao máximo.
Quando um produto é mal produzido aquilo significa um custo para a empresa e, consequentemente, diminui seu lucro.
Para evitar que esse tipo de situação aconteça ou que pelo menos ocorra com o mínimo de frequência possível, as empresas utilizam metodologias. Uma das mais utilizadas é a Six Sigma.
Mas de que adianta utilizar uma metodologia se não fizer uma análise dos dados que estão sendo obtidos?
É nesse ponto que a distribuição de Poisson aparece na organização. Através desse tipo de probabilidade os defeitos passam a ter uma melhor base para serem calculados.
Quando a quantidade de possibilidades desses defeitos acontecerem é grande, Poisson se mostra ainda mais necessário.
Outro ponto que também faz com que essa equação seja utilizada é quando a probabilidade de um defeito ocorrer é pequena. Isso levando em consideração qualquer região do espaço ou até mesmo o instante do tempo.
Conclusão da Distribuição de Poisson
A distribuição de Poisson é considerada uma lei de probabilidade absolutamente discreta, mas de grande utilidade.
Ela descreve a probabilidade de um evento ocorrer durante um determinado intervalo de tempo, quando a probabilidade de um evento ocorrer é bem baixa e a quantidade de tentativas é bastante grande.
Entre suas áreas de predileção, controles de qualidade (incluindo revisão contábil, pois se pressupõe que os erros são raros), probabilidades de inadimplência, acidentes …
Quando se trata de operações complexas que a produção apresenta a utilidade da distribuição de Poisson se torna ainda mais relevante.
São nesses momentos que as oportunidades para que os defeitos apareçam crescem de forma muito rápida.
Assim, a probabilidade de um defeito ocorrer dentro de um tempo específico ou área passa a ser reduzida.