Introdução à Distribuição Normal
A distribuição normal é um dos tipos de distribuições da probabilidade que mais é utilizada, mas não se limita apenas a isso, pois sua importância para a estatística é gigantesca.
Vários conceitos matemáticos estão ligados à distribuição normal, como é o caso da distribuição de Laplace-Gauss e a distribuição gaussiana, por exemplo.
Aliás, Frederick Gauss, no século XIX, observou os eventos da natureza das amostras que estava estudando apresentavam um comportamento padrão.
Tal comportamento é a conhecida Curva de Gauss a qual mostra que a maior parte dos eventos fica próximo ao valor médio com certa variabilidade.
Mas isso é tudo o que tem de similaridade entre os estudos de Frederick Gauss e a distribuição normal? É o que você vai descobrir a seguir!
Tabela de Conteúdo
- O que é a Distribuição normal?
- Como fazer para determinar se a distribuição é ou não normal?
- Teorema Central do Limite
- Como fazer a interpretação da curva de distribuição ?
- Quando a distribuição binomial pode ser utilizada?
- Distribuição estatística discreta e seus tipos
O que é a Distribuição normal?
A distribuição normal e a distribuição gaussiana são exatamente a mesma coisa. Ela se trata de uma curva simétrica que fica em torno do ponto médio. Seu formato é bem interessante e chama muito a atenção, pois é similar ao de um sino.
Quando observamos uma distribuição estatística vemos que ela define uma curva e que a área sob ela determina qual a probabilidade de o evento correlacionado acontecer. Mas a distribuição normal é um tanto diferente disso.
Diversos processos que ocorrem em uma empresa e até fenômenos comuns podem ter seus comportamentos apontados na curva da distribuição normal.
Por exemplo, a pressão sanguínea que um grupo de pessoas apresenta, o tempo gasto por um grupo de funcionários para realizar certa tarefa.
Aliás, as empresas também podem utilizar esse tipo de distribuição não apenas para obter certas informações, mas dentro da metodologia Lean Six Sigma.
Para quem ainda não sabe, Lean Six Sigma é um método que busca promover uma melhora do desempenho através da remoção sistemática do desperdício e da redução da variação.
Assim, quando essa metodologia faz uso das ferramentas matemáticas, ela consegue fazer uma análise e definir quais as estratégias são mais eficientes para promover a melhoria contínua.
Essa distribuição também pode fazer uma aproximação das distribuições discretas existentes na probabilidade, como é o caso da distribuição binomial.
A distribuição normal também pode servir de base para que seja feita a inferência estatística clássica cujos dados apresentam o mesmo valor como a moda, média e mediana.
Quer ser um especialista em Melhoria Contínua? Confira nosso Curso Green Belt EAD!
Como montar uma curva de distribuição normal?
Não há forma melhor de aprender como montar uma curva de distribuição normal que vendo um exemplo prático.
Suponhamos que um professor chegou em uma sala de aula e fez a anotação da idade dos 40 alunos que estavam presentes.
Ao finalizar a coleta dos dados ele conseguiu perceber que a idade daqueles alunos tinha o formato da distribuição normal com o desvio padrão e a média medindo, respectivamente, o=2e e u=23
Agora ele tem como objetivo fazer a projeção da curva da distribuição normal que corresponda a esses valores.
Também precisa determinar a porcentagem de alunos que possuem idade na faixa dos 21 aos 25 anos e os da faixa de 19 a 27 anos. Já se sabe que o valor da média é igual a 23 anos e que ele se encontra no ponto mais alto da curva.
A distribuição normal tem seu começo próximo ao menos três sigma e seu término é próximo ao mais três sigma. Assim, o começo da curva deve começar próximo a 23-3*2 = 17 e seu decaimento ocorre próximo a 23+3*2 = 29.
Os alunos que possuem idade na faixa dos 21 aos 25 anos correspondem a +- 1o que é 68,26% do total de alunos.
Enquanto isso, os alunos que se encontram na faixa etária dos 19 aos 27 anos tem variação de +- 2o o que, em porcentagem, corresponde a 95,44% da totalidade dos alunos. Esse número fica próximo a 38 alunos.
Como fazer para determinar se a distribuição é ou não normal?
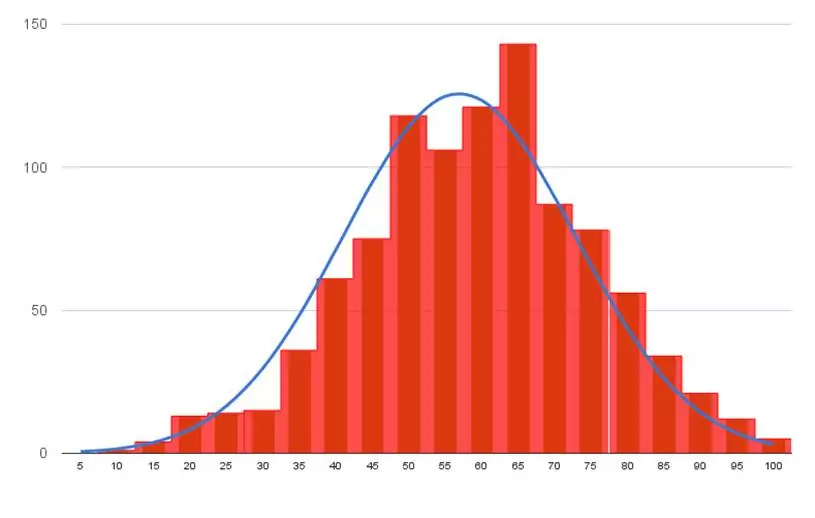
Quando se tem uma variável aleatória e deseja-se saber se ela segue uma distribuição normal é preciso observar se ela segue a função da densidade de probabilidade.
Para isso, é preciso fazer um cálculo utilizando a fórmula a seguir:
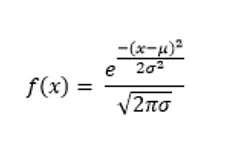
Onde e^2 representa a média da variância de x. Quanto a notação que é utilizada para fazer a denotação de tal distribuição temos:
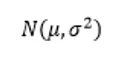
Mas o que isso significa? Quer dizer que para que a probabilidade de certo resultado seja calculada é preciso fazer a integração da função f(x) possuindo como relação a x.
Os limites da integração devem representar a faixa dos valores que se deseja obter a probabilidade.
Vale salientar que a função densidade da probabilidade normal, mais precisamente sua integral, não conta com solução analítica. É por esse motivo que a realização do cálculo deve ser feita utilizando-se um método numérico.
Para que essa dificuldade seja sanada há uma solução: padronizar a função substituindo os parâmetros por o^2 e u=0.
Essa abordagem é possível por causa da definição da nova variável aleatória do conjunto Z que também é conhecida por variável aleatória normal padronizada.
Caso o x seja uma variável aleatória normal que possua média:
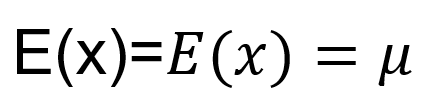
e a variância é:
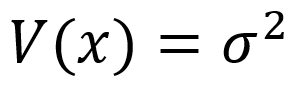
então,
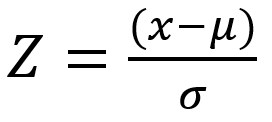
que é uma variável aleatória será normal com o E(Z)=0 e o V(Z)=1. Resumindo, o Z nada mais é que a variável aleatória normal padrão.
Na prática, isso vai permitir obter a área que se encontra sob a curva de normal padrão da forma analítica.
Assim, é possível conhecer a área que existe entre dois pontos que se encontram sob a curva utilizando-se diretamente uma tabela de conversão. Essa área é representatividade da probabilidade.
Teorema Central do Limite
Quando se trata de amostras grandes, o Teorema Central do Limite diz que a distribuição das médias da amostra fica próximas ao que é observado que elas se aproximam normalmente quando distribuídas.
Isso ocorre independentemente do valor da distribuição da variável que se tem interesse.
Elas também tendem a ter uma distribuição normal conforme o tamanho da amostra cresce. A seguinte fórmula é utilizada:
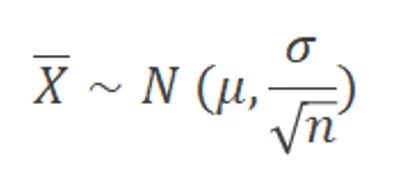
Onde o corresponde a média das medidas individuais do X; o trata-se do desvio padrão encontrado nas medidas individuais do X; n é o tamanho da amostra.
Vamos tomar como exemplo uma empresa que faz a medição da quantidade de defeitos que um lote com 100 produtos apresenta a cada 2 horas.
Com o histograma dos dados que foram coletados no período de duas horas tem-se a representação da distribuição diferente da normal.
Posteriormente, esses dados passaram a ser agrupados diariamente. Isso quer dizer que é realizado o cálculo da média dos defeitos que ocorrem no dia de produção.
O valor encontrado para a média diária passou a ser utilizado para a geração do novo histograma, só que, dessa vez, a distribuição é normal.
Distribuição normal e as perguntas de probabilidade
Em um primeiro momento, podem até parecerem complexas as perguntas quanto à probabilidade da distribuição normal padrão, mas elas são fundamentais.
Mas elas não podem ser deixadas de lado, pois sem a resposta às mesmas é praticamente impossível conseguir a área representada sob a curva.
A área total que se encontra abaixo da curva de distribuição normal padrão corresponde a 100%. Isso quer dizer que o 1 surge como um decimal.
Vamos compreender melhor através de um exemplo. A metade da esquerda da curva corresponde a 50%, o que é o mesmo que dizer que é 0,5.
Isso significa que a probabilidade da variável aleatória está localizada naquela metade da esquerda da curva é de 0,5.
Então todos os problemas que surgirem são simples assim? É claro que não e é por essa razão que é utilizada a tabela-z. Essa tabela mede essas probabilidades e as coloca nos desvio-padrão da média.
Já a média encontra-se no centro da distribuição normal padrão e a probabilidade de 50% corresponde a zero desvios padrão.
Como fazer a interpretação da curva de distribuição ?
O desenho da curva de distribuição normal pode até não ser tão complicado de fazer, afinal, são utilizados apenas a média e o desvio padrão como parâmetros. Entretanto, é preciso saber interpretar essa curva.
Considerando a probabilidade de um fenômeno ocorrer, a área que se encontra abaixo da curva representa os 100%.
Assim, isso significa que a probabilidade de determinada observação ter seu valor entre dois pontos quaisquer corresponde a área que esses dois pontos compreendem.
Na curva há o ponto mais alto e ele representa o valor que possui a maior moda daquele processo, isto é, o valor que naquela base de dados aparece com mais frequência.
Ele é representado com um corte central no diagrama mesmo no ponto alto da curva.
Também são feitos outros cortes verticais, mas eles representam o desvio padrão que foi dado em relação à média.
Resumindo, esta é uma faixa de valores que é dada através da soma ou da subtração do desvio padrão possuindo como relação a média.
Cada faixa com os valores representa certa probabilidade de ocorrer. Se retomarmos o exemplo da sala de aula, temos que na primeira faixa o desvio padrão é menos 1 e segue até o 1 que é o desvio padrão. Isso compreende 68,26% da base dos dados.
O que acontece se for feita uma ampliação pequena?
Caso seja feita uma pequena ampliação para que a faixa que se estende do mais até o menos dois sigma seja pega, a possibilidade de ocorrência sobe para 95,44%.
Mas se a faixa com maior amplitude for pegar nessa distribuição, o que corresponde a mais ou menos três sigma, ela representará 99,74% dos dados.
O nome dessa região é faixa natural de variação do processo. Na estatística existe a compreensão que em um processo há certa variabilidade.
Assim, ela trabalha seguindo uma faixa de valores, mas que possui certa variação. Caso esse processo seja estável então sua variação ocorre dentro da faixa de valores.
Caso haja uma perturbação maior ou algum problema no processo pode significar que o resultado que ele vai produzir não é o que se espera ou então que não havia essa probabilidade.
Resumindo, é preciso observar se o resultado obtido está muito abaixo ou acima do normal.
Como se trata de um resultado que se encontra fora da faixa natural de variação do processo temos o que se chama de ponto fora da curva.
Ou seja, ele é um ponto que a probabilidade de acontecer é tão baixa que recebe a denominação de outlier.
A partir desse entendimento, como ele pode ser comparado e entendido em uma empresa ou processo?
Basicamente, quando a base de dados é representada na curva de Gauss que compreende uma faixa com mais ou menos três sigma quer dizer que aquele processo é estável.
Quando a distribuição binomial pode ser utilizada?

Quando um projeto da metodologia Lean Six Sigma é iniciado é preciso verificar o tipo de dado que está sendo lidado ao sair do processo.
Assim será possível determinar quais ferramentas serão utilizadas enquanto o projeto está sendo desenvolvido.
Inúmeras distribuições estatísticas são realizadas, mas é preciso definir qual delas é a que possui melhor representação do processo estudado.
Essas distribuições dividem-se em distribuição discreta e distribuição contínua, ou atributos e variável, respectivamente.
A utilização das distribuições discretas ocorre quando se deseja modelar as situações em que a saída que se tem interesse pode assumir valores discretos, inteiros.
Um ótimo exemplo é o 0 para falha e o 1 para o sucesso.
Distribuição estatística discreta e seus tipos
Distribuição de Poisson
Quando a probabilidade trata-se de uma distribuição discreta que se aplica às ocorrências que certo número de eventos ocorre em certo intervalo temos a distribuição de Poisson.
Para reconhecer essa distribuição é preciso observar três aspectos:
- São realizados cálculos para determinar quantas vezes um evento aconteceu dentro de certo intervalo de área, volume, tempo etc.
- Não há dependência do número de ocorrências que ocorrem no intervalo.
- Cada intervalo possui a mesma probabilidade do evento acontecer.
Distribuição Binomial
Na distribuição normal há a distribuição binomial que também pode ser utilizada.
Esta última trata-se da distribuição estatística discreta e de probabilidade da quantidade de sucessos que decorreram de certa sequência de tentativas.
Suas características são:
- Somente dois resultados são possíveis em cada tentativa.
- Seu espaço amostral é finito.
- Todos os elementos possuem as mesmas possibilidades para ocorrer.
- Os eventos não dependem uns dos outros.
Conseguiu compreender um pouco mais sobre a distribuição normal? Não deixe de conferir os demais conteúdos do nosso blog!
