Introdução à Estatística Descritiva
A estatística descritiva básica é um dos tipos de estatística descritiva que, por sua vez, é um dos ramos da estatística.

Esta última trata-se de um ramo pertencente à matemática que tem por objetivo realizar uma coleta de dados, analisá-la, interpretá-la e apresentar seus dados numéricos de forma que todos compreendam.
A estatística descritiva se diferencia dos demais tipos de estatística por um simples motivo, seu objetivo é fazer uma descrição e sumarização dos dados que foram coletados.
Ela é diferente da estatística inferencial e da indutiva, por exemplo. Dentro da estatística descritiva existem outros tipos como é o caso do padrão, desvio, mediana e média.
A seguir, vamos aprender um pouco mais sobre a estatística descritiva básica, quando ela pode ser utilizada, quais medidas a compõem e muito mais!
Tabela de Conteúdo
- O que é a Estatística descritiva?
- Medidas de tendência central
- Estatística descritiva básica vs estatística inferencial
- Conclusão da Estatística Descritiva Básica
O que é a Estatística descritiva?
A estatística coleta, analisa, interpreta e apresenta os dados. Mas para que esses passos possam ser dados é preciso iniciar de alguma forma.
A estatística descritiva trata-se justamente da primeira etapa da análise e é utilizada para fazer a descrição e o resumo dos dados.
Essa área ganhou mais vigor após a disponibilização dos métodos computacionais mais eficientes e da grande quantidade de dados.
Várias técnicas são utilizadas para fazer a descrição e o resumo dos dados. Elas também são usadas para estudar o comportamento geral que os dados observados apresentam.
Tudo isso pode ser feito por meio de gráficos, tabelas de frequência e medidas como mediana, moda, média, medidas de dispersão como é o caso do quartis, percentis e padrão.
A descrição que é feita não se dirige apenas aos dados em si, mas às principais tendências que eles apresentam. Essa estatística observa as situações que acabam levando a novos fatos.
É por esse motivo que esse método não tem hipótese e se baseia em uma ou algumas questões de pesquisa.
Por se tratar da etapa inicial, a estatística descritiva básica conta com uma quantidade grande de dados e também de métodos computacionais que possuem uma eficiência gigantesca.
Tudo isso permite que ela seja usada em conjunto com a metodologia Lean Six Sigma.
Assim, a estatística descritiva básica acaba por auxiliar a metodologia Six Sigma a analisar os dados de sua aplicação.
Quando a estatística descritiva pode ser usada ?
A estatística descritiva básica comumente é utilizada quando há uma grande quantidade de informações que precisam ser condensadas para que seja possível trabalhar com elas.
Para fazer isso existem algumas formas muito interessantes, como as medidas de posição da estatística descritiva que também é chamada de medidas de tendência central.
Esse tipo de medida indica onde os dados estão localizados. Divide-se em média, moda, mediana, percentis e quartis.
Já as medidas de dispersão da estatística descritiva permitem fazer uma avaliação quanto aos dados, verificar se sua distribuição ocorreu conforme o padrão desejado.
O objetivo principal disso é conseguir encontrar um valor que seja capaz de resumir a variabilidade que determinado conjunto de dados possui.
Quer saber mais sobre a Estatística Descritiva? Confira nosso Treinamento Online de Green Belt!
Medidas de tendência central
A seguir, vamos ver os cálculos mais usados na estatística descritiva básica e usaremos exemplos para facilitar o entendimento
Média
Para encontrar a média basta somar todos os valores que estiverem na base de dados e dividir pela quantidade de elementos totais utilizados nessa soma.
A fórmula da média é a seguinte:

Dentro da média há a média ponderada. Nesse caso, cada dado é multiplicado por um valor que é chamado de peso. Os elementos são somados e divididos pela soma dos pesos como está descrito a seguir:
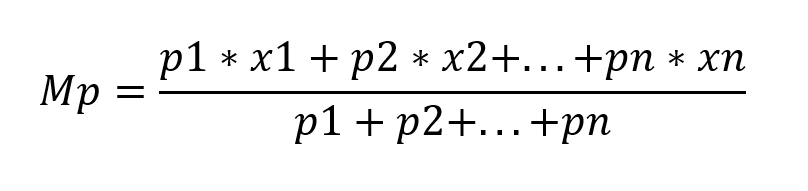
Por exemplo, uma fábrica de garrafas realizou a coleta de dados por alguns dias a fim de saber quantas garrafas são perdidas por dia. O resultado foi o seguinte:
- Quantidade de garrafas perdidas em cada dia: 5, 9, 10, 4, 7, 5, 2, 5, 5, 12, 4, 8, 3.
Para realizar a média aritmética basta somar todos eles e dividir pela sua quantidade, dessa forma:
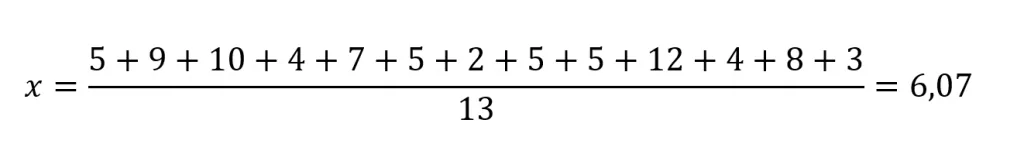
Isso quer dizer que a média de garrafas que são perdidas diariamente corresponde a 6,07.
Moda
Moda de um número significa que ele é o que aparece com maior frequência na base de dados.
É importante salientar que nenhum valor presente na base de dados deve se repetir e, por esse motivo, a moda não existirá nesse caso.
Se pegarmos o exemplo dado anteriormente vemos que o número 5 aparece com frequência e, portanto, é a moda.
Mediana
A mediana trata-se do termo central que existe em um conjunto de dados que são colocados na ordem crescente ou na ordem decrescente. Ou seja, é uma medida do posicionamento central.
Caso a quantidade dos valores ordenados seja ímpar a mediana será exatamente aquele número que encontra-se no meio da lista.
Mas se essa quantidade for par, a mediana será calculada como uma média entre dois valores que se encontram no centro.
Continuando com nosso exemplo, sabemos que a quantidade de garrafas perdidas em cada dia é: 5, 9, 10, 4, 7, 5, 2, 5, 5, 12, 4, 8, 3.
Para que a mediana seja determinada esses dados precisam estar ordenados de forma decrescente ou crescente. Se colocarmos na ordem decrescente ele ficará assim:
- 12, 10, 9, 8, 7, 5, 5, 5, 5, 4, 4, 3, 2.
Como temos um número ímpar de amostras, a mediana será aquela que se encontra ao centro, no nosso caso, o número 5. Mas, suponhando que o número 2 não fizesse parte da lista, teríamos um conjunto de amostra par.
Nesse caso, teria que ser feita a média dos dois valores centrais que seriam 5 e 5 e o resultado seria 5.
Percentis
A estatística descritiva básica é auxiliada também pela Percentis que trata-se das medidas que fazem a divisão da amostra em cem partes iguais.
A amostra deve estar na ordem decrescente e cada uma das partes deve ter uma percentagem aproximadamente igual de dados.
Assim, temos:
- O 98º percentil vai determinar os 98% menores relativo aos dados
- O 50º percentil vai determinar os 50% menores relativo aos dados e é igual ao valor da mediana
- O 1º percentil vai determinar o 1% menor relativo aos dados.
A fórmula que realiza o cálculo do percentil é:
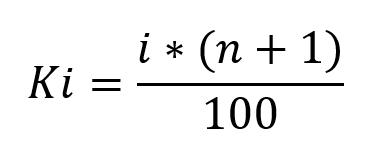
Onde K é a posição do percentil nos dados; i é o percentil desejado e n é o número de amostras.
Vamos ver através de um exemplo prático. Suponhamos que na seguinte amostra: 8, 3, 12, 4, 5, 5, 2, 5, 8, 4, 7, 10, 5, 9 deseja-se encontrar 40º percentil.
Primeiramente é feita a ordenação dos dados: 2, 3, 4, 4, 5, 5, 5, 5, 7, 8, 8, 9, 10, 12. Realizando o cálculo temos:
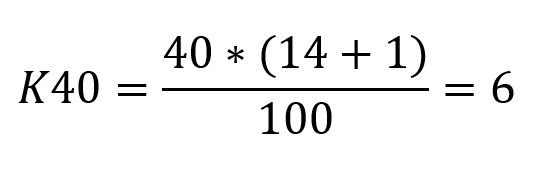
Isso quer dizer que o percentil está localizado na 6ª posição e que, portanto, corresponde ao valor 5.
Quartis
Quartis são os valores que fazem a divisão em quatro partes iguais dos dados ordenados. Com ele, a dispersão pode ser avaliada rapidamente bem como a tendência central existente em um conjunto das amostras.
A fórmula do quartil é a seguinte:
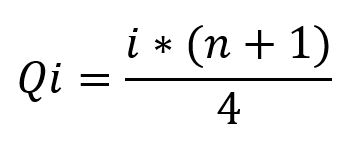
Onde Q é a posição do quartil nos dados; i é o quartil que se pretende encontrar e n é o número das amostras.
Por exemplo, na amostra 8, 3, 12, 4, 5, 5, 2, 5, 8, 4, 7, 10, 5, 9 desejamos encontrar o 4º quartil. Após a ordenação ela fica: 2, 3, 4, 4, 5, 5, 5, 5, 7, 8, 8, 9, 10, 12.
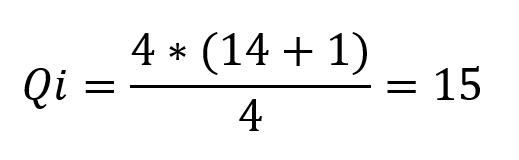
Ou seja, o quartil encontra-se na 15ª posição. Caso o resultado tivesse sido em decimal e não em inteiro, seria necessário uma média entre a posição inteira e a imediatamente acima, ou seja, 15 e 16.
Amplitude
A amplitude mostra o quão espaçado os dados são ou não na amostra trabalhada no momento. Esta é a maneira mais simples de analisar a dispersão dos dados.
O valor da amplitude em certo conjunto de amostras é dado a partir da diferença entre aqueles que apresentam maior e menor valor.
Caso a amplitude seja elevada quer dizer que os dados possuem um intervalo grande de distribuição. Caso seja reduzido, significa que esses intervalos são pequenos.
Podemos pegar nosso exemplo anterior para encontrar a amplitude. Assim, os dados ordenados ficam 2, 3, 4, 4, 5, 5, 5, 5, 7, 8, 8, 9, 10, 12.
A=12 – 2= 10, ou seja, 10 é a amplitude dessa amostra.
Intervalo-interquartil
O objetivo do intervalo interquartil é fazer uma análise do grau de dispersão ao redor da medida da centralidade dos dados.
Seu cálculo é feito por meio da diferença entre os quartis terceiro e primeiro.
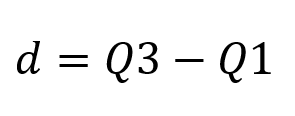
Pegando novamente nossa amostra dos exemplos anteriores a fim de ter o intervalo-interquartil, teremos: 2, 3, 4, 4, 5, 5, 5, 5, 7, 8, 8, 9, 10, 12.
Devemos encontrar o terceiro quartil para realizarmos o cálculo do intervalo-interquartil:
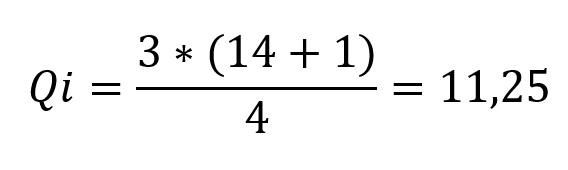
Para obter o valor do quartil é preciso fazer uma média entre as posições 11 e 12 que resultará em:
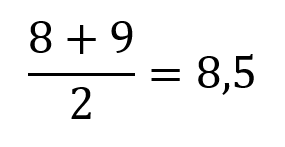
O primeiro quartil também deve ser calculado:
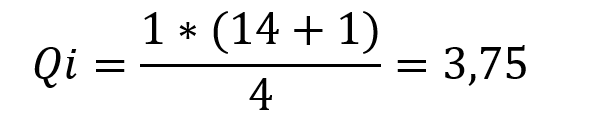
Para a obtenção do primeiro quartil é preciso encontrar a média dos valores referentes a terceira e quarta posição:
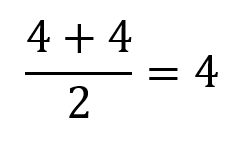
Assim, o intervalo-interquartil corresponde a:
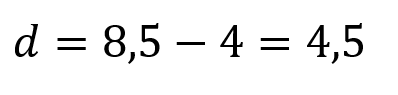
Variância
A variância também é um cálculo que contribui para a estatística descritiva básica. Afinal, ela mostra o quanto os valores presentes na amostra encontram-se em relação à média.
Sua fórmula é dada por:
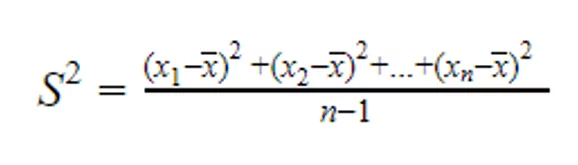
Onde S^2 é a variância; n é a quantidade de amostras e x é a média que as amostras possuem.
Vamos supor que temos a amostra 10, 7, 5, 4, 9 e desejamos encontrar sua variância. Devemos realizar sua média:
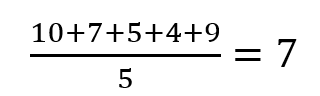
E depois calcular:
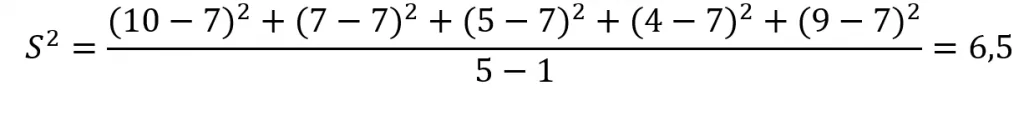
Desvio Padrão
A medição do Desvio padrão faz a indicação do grau de dispersão que a amostra apresenta em relação a média.
Seu cálculo faz uso da variância, mais precisamente da sua raiz quadrada como observado na fórmula a seguir:
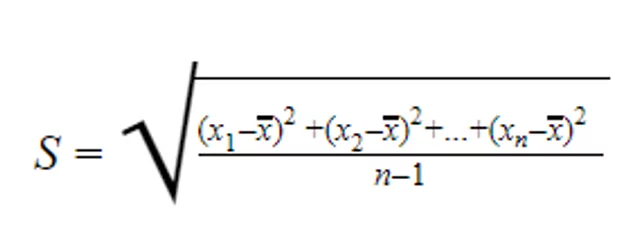
Onde S é o desvio padrão; n é o número das amostras e x é a média das amostras.
Continuando com nosso último exemplo de amostra, 10, 7, 5, 4, 9, para encontrar o desvio padrão teremos que encontrar a média:
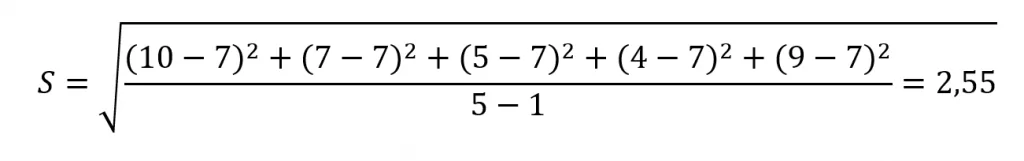
Coeficiente de variação
O coeficiente de variação é uma medida que a dispersão relativa possui e que é muito útil para fazer a comparação entre duas variáveis ou mais.
Para fazer seu cálculo utiliza-se a fórmula:
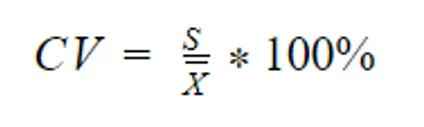
Tomando nosso exemplo anterior para calcular o coeficiente de variação teremos:

Estatística descritiva básica vs estatística inferencial
Dentro da estatística existem diversos tipos e a estatística descritiva básica e a estatística inferencial são bastante populares.
Apesar de pertencerem à mesma família, esses tipos de estatística possuem características diferentes.
A estatística inferencial utiliza as informações da amostra com o intuito de chegar a uma conclusão relativa ao grupo maior que não se tem acesso.
Por esse motivo, a probabilidade é a ferramenta que comumente é utilizada dentro da estatística inferencial.
Já a estatística descritiva básica envolve o resumo, a representação dos dados e a organização deles.
Para isso, ela faz uso de diversas ferramentas como gráficos, diagramas como o diagrama de Venn, média, moda, mediana, variância, desvio padrão e coeficiente de variação, por exemplo.
Conclusão da Estatística Descritiva Básica
A estatística descritiva básica é um dos tipos de estatística. Ela vai organizar os dados da amostra no início da análise.
Para isso, diversas ferramentas podem ser utilizadas para esse intuito, como é o caso do diagrama de Venn, média, mediana, moda, desvio padrão e muitas outras.
Você sabia da existência da estatística descritiva básica? O que achou dela e das suas ferramentas? Deixe seu comentário!
