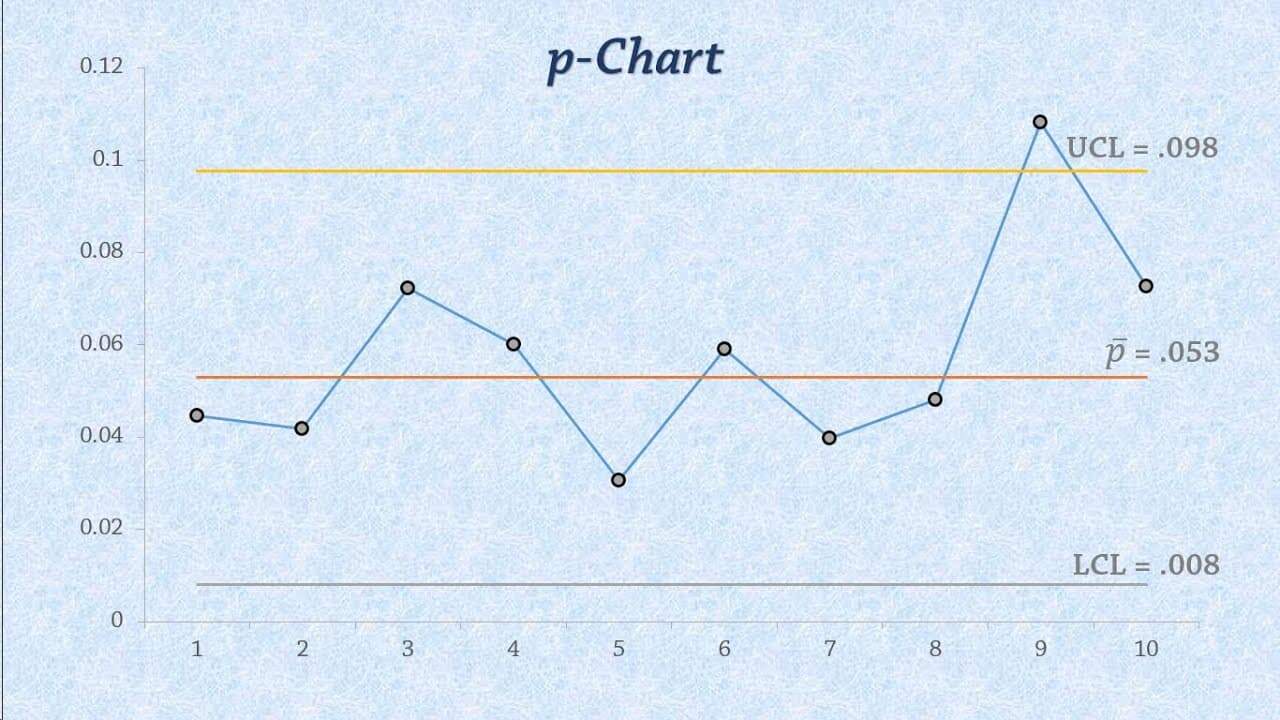
Gráfico p : Saiba o que é e como utilizar
O gráfico P é um dos gráficos de controle mais utilizados para a realização de análise de dados em um determinado processo.
Sendo um dos gráficos utilizados na área de Controle Estatístico de Processo, ele pode ser bastante útil na resolução de problemas caso seja bem aplicado.
Tabela de Conteúdo
- O que é um gráfico p?
- Como o gráfico p se comporta?
- Como construir o gráfico p?
- Exemplo da aplicação do gráfico p
- Conclusão sobre o gráfico p
O que é um gráfico p?
O gráfico de pontos, gráfico de preço ou gráfico de proporção de defeitos é uma das maneiras mais comuns de se chamar o gráfico de P.
Ele pode ser definido como um gráfico de controle que é muito utilizado para, ao longo do tempo, controlar a porcentagem de itens defeituosos de uma determinada classificação em um conjunto de dados.
O gráfico P é um gráfico atemporal, ou seja, não depende de um tempo específico para que ele se forme. Esse tipo de gráfico é muito versátil para índice de dólar e em ativos que há muita briga e posicionamento de players nos preços.
Com ele, é possível analisar faixas de preço em que o mercado tende a permanecer e que, caso sejam rompidas, geram muitas oportunidades de trades.
Mas além do mercado financeiro? O que de fato é o gráfico P na área de análises estatísticas?
Bom, esse gráfico é uma ferramenta muito importante para analisar dados (sendo um ponto central da metodologia Seis Sigma).
Quando há um indicador como uma variável de classificação, um dos gráficos mais adequados é o gráfico P, pois ele é um conhecimento essencial para todo Green Belt e Black Belt na metodologia Seis Sigma.
Sendo assim, esse tipo de gráfico é bastante utilizado em processos que produzem itens defeituosos (mesmo quando há controle), são muito usados em controle de qualidade de serviços, produção de itens com pequenos defeitos que podem ser sanados e produção de itens com alguns pequenos defeitos que não utilizam o todo.
Como o gráfico p se comporta?
O gráfico P é muito simples de interpretar, pois é preciso apenas procurar por pontos fora de controle, ou seja, pontos que fujam dos padrões no processo e que ultrapassem os limites superiores e inferiores do gráfico.
Os limites de controle podem mudar nos gráficos P e U, pois depende dos diferentes tamanhos de amostra utilizados para cada ponto plotado.
Se o tamanho da amostra não variar em mais de 15%, o controlador do gráfico poderá usar o tamanho médio da amostra nesses gráficos para determinar os limites de controle comuns para todas as amostras.
Normalmente essa é uma opção no SPC (Statistical Process Control), que no português, é traduzido como Controle Estatístico de Processo. Caso hajam mudanças repentinas, elas devem ser reparadas da seguinte forma:
- É necessário fazer um brainstorming e conduzir os experimentos projetados a fim de encontrar elementos do processo que acabem contribuindo para mudanças esporádicas no local do processo;
- É preciso remover o viés estatístico dos pontos fora de controle, com a finalidade de retirá-los dos cálculos da linha central do processo e de seus limites de controle.
É importante também entender quais são as condições necessárias para que o gráfico seja construído.
A construção dos gráficos p só é possível se as seguintes condições forem feitas:
- Tamanho amostral constante;
- Tamanho amostral variável;
- Com a média amostral;
- Com a média dos defeituosos.
Como o gráfico pode ser utilizado?
O gráfico P pode ser utilizado quando precisamos realizar iniciativas de controle da qualidade com dados do tipo atributo discreto.
Esses dados não podem ser mensurados de forma numérica, sendo definidos como dados do tipo passa ou não passa, ruim ou bom, alto ou baixo e entre outros.
A utilização do gráfico P pode ser feita para:
- Avaliação da necessidade de estratificação em subgrupos (local, funcionário, hora ou dia);
- Plotar a proporção de dados em uma categoria específica. Não é necessário ter tamanhos iguais de amostras para cada ponto de dados, porém, poderá usar uma variação do gráfico P chamada de gráfico np.
Os dados de proporção são plotados, normalmente, para que os líderes dos negócios possam determinar se o desempenho do processo estava estável ou instável;
- Constatar possíveis mudanças repentinas nos sistemas que provavelmente podem ser atribuídas a alguma causa;
- Mostrar se o sistema está sendo estável, ou seja, sem causas especiais e sob controle;
- Iniciativas de controle de qualidade quando os dados forem do tipo de atributo discreto (mais conhecido como dados categóricos). Se os dados forem obtidos através do agrupamento de instâncias em categorias específicas, irá desenvolver dados de atributos discretos;
- É capaz de comparar os sistemas antes e depois de acontecer alguma mudança, como os horários das centrais de atendimento antes e depois do treinamento dos funcionários, por exemplo;
- Identificar a ocorrência de causas especiais, para que possam ser removidas, com uma redução na variação geral do processo;
- Não são muito úteis para o rastreamento de tendências ao longo do tempo ou mudanças no processo;
- Podem ser utilizados para comprovar o impacto de algumas mudanças em um sistema;
- Auxiliam na tomada de decisão dos líderes de negócio, pois eles ajudam a visualizar se o processo está estável ou não, sendo possível verificar se há causas especiais, atuando assim na eliminação desse problema para que decisões mais eficientes sejam tomadas;
- Inclui limitações de controle superior e inferior estatisticamente determinadas, indicando os limites do comportamento esperado do processo.
Quais dados são mostrados nesse tipo de gráfico?
Sabemos que na prática podemos fazer um gráfico utilizando diversos tipos de dados para atingir um determinado objetivo.
No entanto, para que usar um gráfico P, é necessário que os itens desse tipo de gráfico atendas a duas condições, sendo elas:
- É necessário ter um número limitado no uso de dados do gráfico P, ou seja, não podemos fazer uso de quantidade de dados desconhecidas ou ilimitadas, é necessário definirmos o número de amostras a serem analisadas;
- A probabilidade de falha deve ter consistência em todos os itens da amostra.
Supondo que o tempo médio de atendimento excede 20 minutos, que seria uma falha, a 10% do tempo, e você possui algum tipo de prioridade de atendimento, o gráfico P não poderá ser utilizado, pois não há consistência de falha em todas as amostras, já que alguma pode ter se favorecido por conta dessa prioridade de atendimento.
Antes de realizar o mapeamento dos dados, é necessário definir algumas normas para o seu sistema.
Você deve fazer uso de dados em um sistema que esteja sob controle, com variáveis estáveis, encontrando dessa forma a probabilidade média (p) e os limites inferiores e superiores de controle para os defeitos aceitáveis.
Após o estabelecimento dessas normas já é possível plotar um novo sistema com os dados.
Como construir o gráfico?
O gráfico P é construído com base no número de itens com defeitos (que fogem das conformidades) na amostra dividido pelo número total de itens da amostra.
O valor de amostra p se registra como uma fração de tamanho do subgrupo.
Essa fração de itens não conformes pode se referir às amostras que possuem tamanhos fixos definidos e coletados de modo regular ou até mesmo podem se referir a 100% da produção de um item em um determinado período, como por exemplo a produção de um item em 1 hora de produção, 1 dia ou 1 mês, a depender do processo e de suas necessidades.
Sendo assim, isso significa que os subgrupos podem ter tamanhos variados, o que ocorre por conta da variabilidade do tamanho da amostra. Como consequência, os limites de controle também passam a ter uma amplitude variável.
Um item, para ser caracterizado como com defeito ou sem defeito, depende da observação de uma ou várias características relacionadas à qualidade.
Com isso, o item produzido pode ter vários tipos de não conformidades e em diversas situações será muito importante a classificação das não conformidades por relevância diferenciada, sugerindo assim a utilização de gráficos como o gráfico P.
Vale lembrar que o gráfico de proporção de defeitos pode ser construído da seguinte maneira:
1 – Tamanho da amostra constante;
2 – Tamanho da amostra variável;
3 – Com a média da amostra (¯n);
4 – Com a média das não conformidades (¯p).
Esse tipo de gráfico projeta a proporção de defeitos com base em dados de uma determinada categoria.
Não é necessário ter tamanhos de amostras iguais para cada ponto de dado, mas caso prefira, é possível usar uma variação do gráfico P, denominado como gráfico np.
Além disso, antes de iniciar a construção do gráfico é necessário realizar todo o desenvolvimento dos cálculos estatísticos relacionados aos dados de amostra que desejamos construir o gráfico P.
O gráfico só poderá ser construído caso n * p ≥ 5 e n * (1 – p) ≥ 5.
Como realizar a interpretação correta?
Todo gráfico de controle de atributo possui limites de controle superiores e inferiores que são definidos de modo estatístico, indicando assim os limites do comportamento esperado pelo processo, fazendo com que seja possível identificar anormalidades, que são os pontos que ultrapassam esses limites.
A flutuação de pontos entre os limites do gráfico acontece por conta das variações que ocorrem durante o processo.
Essa variação ocorre por conta de causas comuns que acabam influenciando o processo e os pontos que variam acima dos limites são as causas especiais, que são causadas por mudanças no processo.
Sendo assim, podemos concluir que quando um processo sofre apenas influências de causas comuns, ele se torna estável e previsível. Ao identificar causas especiais em um processo é necessário eliminá-las com uma redução na variação geral do processo.
Após a eliminação da causa especial, podemos aprimorar o processo ao realocá-lo a um nível mais adequado ou com a diminuição da variação por conta das causas comuns.
De modo geral, os gráficos de atributos são fáceis de interpretar, pois basta procurar por pontos que ultrapassam os limites de controle.
Em caso de causas especiais, é necessário analisar e entender porque elas acontecem e atuar na sua eliminação.
Exemplo da aplicação do gráfico
Uma fábrica de especiarias apresentou os seguintes dados quanto ao número de pacotes com não conformidades.
A tabela a seguir possui uma amostra n=50 e m=19.
| Amostra | Número de não conformidades (Di) | Fração de não conformidades (pi) |
| 1 | 5 | 0,1 |
| 2 | 15 | 0,3 |
| 3 | 10 | 0,2 |
| 4 | 4 | 0,08 |
| 5 | 3 | 0,06 |
| 6 | 20 | 0,4 |
| 7 | 11 | 0,22 |
| 8 | 9 | 0,18 |
| 9 | 3 | 0,06 |
| 10 | 20 | 0,4 |
| 11 | 11 | 0,22 |
| 12 | 6 | 0,12 |
| 13 | 7 | 0,14 |
| 14 | 11 | 0,22 |
| 15 | 3 | 0,06 |
| 16 | 3 | 0,06 |
| 17 | 9 | 0,18 |
| 18 | 3 | 0,06 |
| 19 | 8 | 0,16 |
Com relação à tabela acima, basta aplicarmos os cálculos para formação do gráfico. Vale lembrar que se a fração de não conformidades não fosse apresentada, seria possível encontrar os respectivos valores dividindo o número de não conformidades pela quantidade total de amostra, que nesse caso é 50.
Depois da tabela estar pronta, devemos fazer o somatório das frações de não conformidades, dividindo o seu resultado pelo m. Ou seja:
p = ∑pi / m
3,22 / 19 = 0,1694
Aplicamos a fórmula de verificação para grandes amostras.
n * p = 50 * 0,1694 = 8,47 ≥ 5
n * (1 – p) = 50 * (1 – 0,1694) = 41,53 ≥ 5
Com esses dados podemos aplicar nas fórmulas para encontrar o LSC (Limite Superior de Controle) e LIC (Limite Inferior de Controle). O LC (Limite Central) é o valor de p.
LSC= p +3 [(p(1-p)/(n)]^(1/2) = 0,1694 + 3 [(0,1694)(1-0,1694)/50]^(1/2)=0,32
LIC= p – 3 [(p(1-p)/(n)]^(1/2) = 0,1694 – 3 [(0,1694)(1-0,1694)/50]^(1/2) = 0,01
Após encontrarmos os limites, podemos fazer um gráfico por meio de softwares como o excel ou até mesmo da forma tradicional, com papel e caneta na mão.
O gráfico P para o nosso exemplo, criado no excel, se comporta da seguinte maneira.
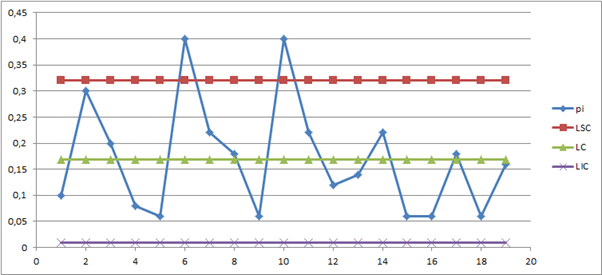
É possível notar que há causas especiais na amostra 6 e 11 e devemos agir para removê-las do nosso processo.
Portanto…
O gráfico P é uma excelente ferramenta do Controle Estatístico de Processo quando desejamos realizar uma análise de dados.
Profissionais da área da qualidade, que atuam com metodologias estatísticas como o six sigma e são certificadas em Green Belt ou Black Belt são os que mais usam tais ferramentas.
Agora que você já sabe como usar e criar esse gráfico de controle nunca mais terá dificuldade para analisar dados no seu processo.