O que é o BOXPLOT e como ele pode ser utilizado?
Sabemos que compreender gráficos não é tarefa fácil e construí-los a partir de cálculos também não é fácil, mas com muita prática e dedicação é possível utilizar a técnica do boxplot.
Esse método também chamado de “box” e “whisker plot” é uma alternativa para os histogramas comuns e para representar os dados de forma visual.
Ele permite reunir e apresentar dados de maneira fácil e bem calculados evitando perdas de dados e análises.
As informações tornam-se mais exatas na ilustração desse tipo de gráfico, resumindo de maneira dinâmica uma visão mais acessível sobre números, taxas, localização e evolução de dados.
O uso desse tipo de gráfico formal tem crescido nas principais empresas, principalmente, nas corporações dedicadas à administração, gestão e análise de mercado.
Na língua portuguesa, esse tipo de gráfico também é conhecido como diagrama de caixa e já é muito popular nas empresas e instituições brasileiras.
O que é boxplot?
O diagrama de caixa refere-se a um método de representação de dados e informações exatas. Ele oferece a capacidade de apresentar informações e características referentes a localização, dispersão, assimetria, comprimento da cauda e outliers.
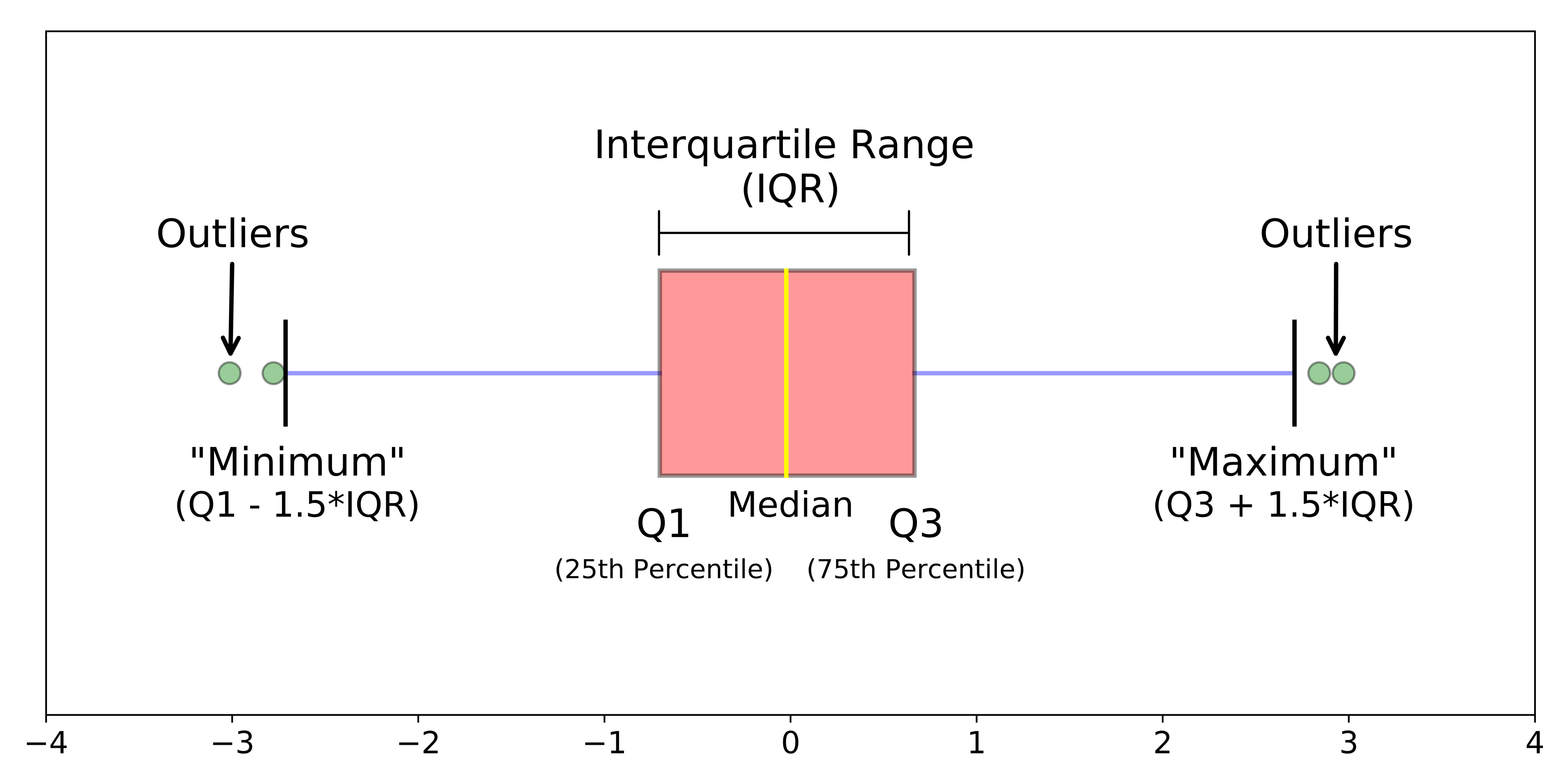
O termo “outliers” refere-se aos dados discrepantes também possíveis de serem abordados no diagrama de caixa.
Mas, vale ressaltar que, mesmo tendo a possibilidade de passar informação sobre localização e dispersão, a verdade sobre o valor está na informação da cauda da distribuição.
Análises e interpretações iniciais
Esse tipo de diagrama possibilita vários tipos de observações e análises. Os outliers, por exemplo, podem influenciar de diferentes maneiras as decisões a serem tomadas a partir da análise dos dados.
É essencial que cada dado seja considerado e analisado corretamente para evitar interpretações erradas.
Geralmente, tendo ou não outliers esse tipo de diagrama pode ajudar a identificar a existência de possíveis outliers no conjunto de dados, desde que estejam calculados e mensurados.
Para as estatísticas
Esse tipo de diagrama é usado para a apresentação estatística e cálculos fundamentados em dados.
É uma importante ferramenta gráfica para representar a variação de dados observados de uma variável numérica por meio de quartis.
Geralmente, o boxplot apresenta uma reta, também referida como whisker ou fio de bigode, cujo traço pode se estender verticalmente ou horizontalmente a partir da caixa, indicando a variabilidade fora do quartil superior e do quartil inferior.
Num conceito mais prático, os outliers apresentarão sempre valores atípicos ou discrepantes podendo ser apresentados (ou plotados) em como pontos individuais.
Características do Diagrama de Caixa
Vale lembrar que o boxplot não é paramétrico, apresentando a variação em amostras de uma população estatística sem fazer qualquer suposição da distribuição estatística subjacente.
Assim, cada espaço existente entre as diferentes partes de cada caixa é usado para indicar o grau de dispersão, além da obliquidade nos dados e os outliers.
Quais são as possibilidades quando usamos Boxplot?
Esse tipo de diagrama permite estimar visualmente vários valores e dados, podendo identificar onde estão localizados 50% dos valores mais prováveis, a mediana e os valores extremos
Sendo muito usada para a análise e comparação de variação de dados variáveis entre diferentes grupos de dados. Parece complexo, porém o que norteia cada traço são os dados e a evolução dos cálculos.
Continue lendo: Tenha acesso a 21 planilhas de Excel, que vão te ajudar a analisar dados!
A história da importância dos Gráficos
Sabemos que desde a Grécia Antiga, nos anos 300 e 250 A.c, a matemática daquela época já utilizada imagens para representar números. As antigas civilizações já usavam imagens como forma de representação fundamental.
Com o passar dos séculos, mais notadamente depois da Revolução Industrial, os matemáticos desenvolveram o uso de gráficos para ajudar em cálculos mais complexos.
Não podemos esquecer do trabalho de pensamento e aplicação matemática de René Descartes, esse estudiosos, depois de anos desde o surgimento da geometria moderna, publica a obra “A Geometria” em 1637.
Nessa obra, René Descartes, que era filósofo e matemático, introduziu o sistema de coordenadas cartesianas, onde cientistas e matemáticos passaram a usar gráficos para informar e educar com a criação de diferentes tipos de gráficos.
O trabalho de Descartes influenciou as populares pizzas gráficas e infográficos dos dias atuais.
Leia mais: Descubra como o Gráfico PERT pode auxiliar no gerenciamento de projetos!
Como o boxplot é usado na educação?
O uso de boxplot também é muito comum na educação, no ensino fundamental, médio e superior nas universidades de exatas.
Vale lembrar que um dos primeiros registros de uso de gráficos na educação vem do matemático Joseph Priestley, falecido em 1804.
Na época, ele utilizou gráficos semelhantes ao diagrama de Gantt para ajudar a lecionar história na Warrington Academy.
Por outro lado, um dos primeiros registros de uso de gráficos na informação vem da enfermeira Florence Nightingale que havia utilizado gráficos polares para mostrar o número de mortes dentro do exército.
A evolução
Com o passar do século XX, a apresentação de dados através de gráficos evoluiu, principalmente, com a evolução da indústria gráfica e da revolução digital que permitiu levar informações gráficas para um público cada vez maior.
Ainda no ano de 1969, John W. Tukey, matemático falecido em 2000, popularizou o boxplot.
Como matemático, Tukey é pioneiro no processo de análise exploratória de dados, tendo desenvolvido várias técnicas para melhorar a visibilidade e a compreensão dos dados.
Ele desenvolveu diferentes técnicas para aprimorar a visibilidade e a compreensão dos dados, incluindo o diagrama ramo e folha, o five number summary e o próprio boxplot.
Aplicações gerais
Desde então, o uso do diagrama de caixa evoluiu bastante em diferentes ciências quantitativas, podendo ser aplicado como gráfico estatístico padrão, aparecendo em grande parte dos textos estatísticos introdutórios.
Como relatado anteriormente, o boxplot teve precursores sob diferentes nomes como o gráfico rangebars e os diagramas de dispersão na geografia e na climatologia
Na atualidade
Atualmente, ele é considerado uma forma rápida para examinar um ou mais conjuntos de dados de maneira visual e gráfica.
Ele possui vantagens sobre as estimativas de densidade kernel por prover mais dados além da mediana (média).
Em seu plano de dados no kernel, a seleção do número e da largura das barras pode influenciar muito na aparência do histograma além da estimativa de densidade kernel, o que não ocorre no diagrama de caixa.
Assim a largura do boxplot pode até ser usada como uma medida de informação dos dados, representando em alguma proporção o tamanho do conjunto de dados referidos.
As estatísticas
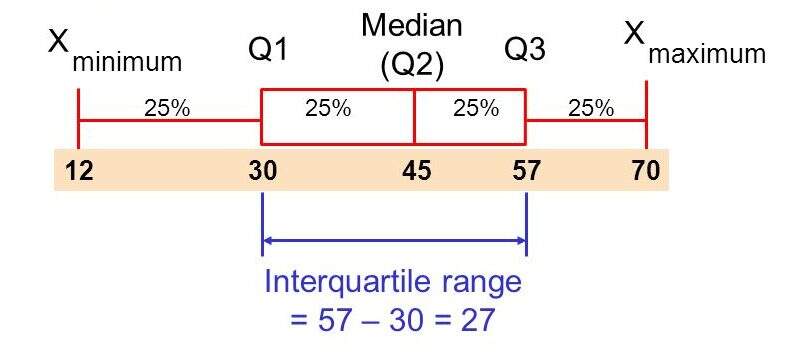
Um gráfico de boxplot pode ser apresentado em cinco estatística, sendo o o mínimo, o primeiro quartil (Q1), a mediana, o terceiro quartil (Q3) e o máximo.
No desenho do gráfico, esses pontos também são chamados de resumo dos cinco números.
Como desenhar?
O traçado não precisa ser uma obra de arte, mas deve ser exato e apto a receber os dados. Em sua construção, é necessário desenhar o retângulo alinhado verticalmente (ou horizontalmente) com duas semirretas, uma em cada um dos lados opostos do retângulo.
Lembramos que a ‘A’ altura do retângulo é definida pelos quartis Q1 e Q3. Uma linha secciona o retângulo no valor da mediana (ou Q2).
Indicamos que as semirretas ligam respectivamente os quartis Q1 e Q3 ao valor mínimo e ao máximo do conjunto de dados.
Outros formatos
Lembramos que o diagrama de caixa pode ser desenhado de diferentes maneiras dependendo do tipo e apresentação de cada dado. Dessa maneira, não há uma única forma de apresentar um gráfico Boxplot.
É possível usar variações na apresentação dos pontos extremos com diferentes quantidades de pontos.
Interpretações possíveis
Outro fator importante são as interpretações. Depois de analisar os pontos e dados, é importante saber tirar conclusões sobre o centro dos dados (a média ou mediana), a amplitude dos dados (máximo – mínimo), a simetria ou assimetria do conjunto de dados e a presença de outliers. Lembrando que “outliers” são as discrepâncias, e quando eles aparecem eles são apresentados com asteriscos.
A dispersão, em determinados casos pode ser representada através da amplitude do gráfico, que pode ser calculada como máximo valor ou mínimo. Assim, quanto maior for a amplitude, maior a variação nos dados.
A posição da linha mediana no retângulo informa sobre a assimetria da distribuição. Uma distribuição simétrica teria a mediana no centro do retângulo. Porém, se a mediana é próxima de Q1, então, os dados são positivamente assimétricos, entre outros fatores variáveis.
A seguir vamos apresentar os conceitos dos componentes referentes aos dados:
– Posição – Em relação à posição dos dados, observa-se a linha central do retângulo (a mediana ou segundo quartil).
– Dispersão – A dispersão dos dados pode ser representada pelo intervalo interquartílico que é a diferença entre o terceiro quartil e o primeiro quartil (tamanho da caixa), ou ainda pela amplitude que é calculada da seguinte maneira: valor máximo ou valor mínimo.
Mesmo que a amplitude seja de fácil entendimento, o intervalo interquartílico é uma estatística mais robusta para medir variabilidade uma vez que não sofre influência de outliers.
– Simetria – Um conjunto de dados que tem uma distribuição simétrica, terá a linha da mediana no centro do retângulo.
Em certos casos, quando a linha da mediana está próxima ao primeiro quartil, os dados são assimétricos positivos e quando a posição da linha da mediana é próxima ao terceiro quartil, os dados são assimétricos negativos.
A mediana é a medida de tendência central mais indicada quando os dados possuem distribuição assimétrica, uma vez que a média aritmética é influenciada pelos valores extremos.
– Caudas – As linhas que vão do retângulo até aos outliers podem fornecer o comprimento das caudas da distribuição.
– Outliers –Estes indicam possíveis valores discrepantes acima do normal. No diagrama, as observações são consideradas outliers quando estão abaixo ou acima do limite de detecção de outliers.
Em quais softwares posso fazer o BoxPlot?
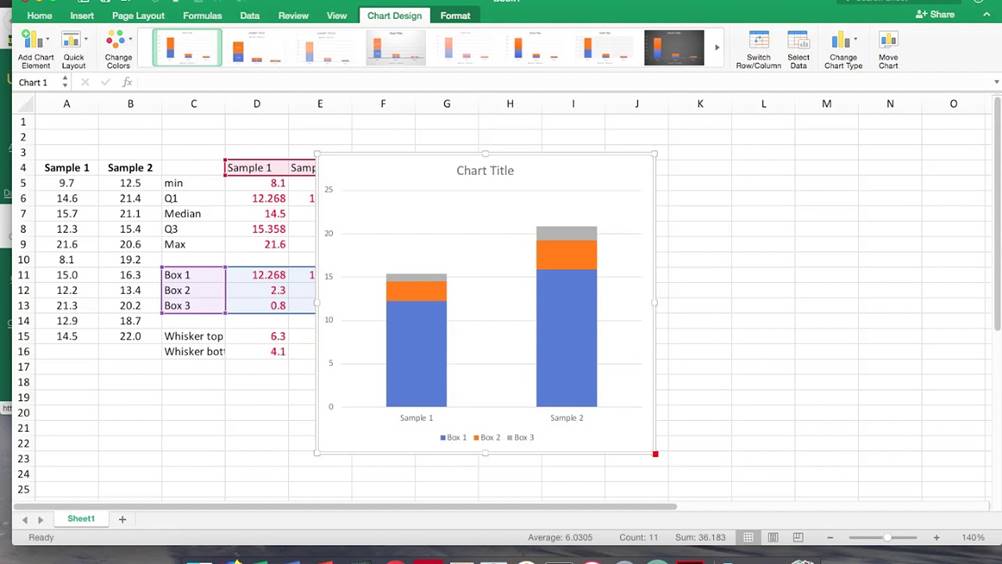
O diagrama de caixa pode ser feito em programas de computador como Excel e Minitab.
Esses programas usam cálculos integrados à imagem do gráfico, pois as medidas podem ser apresentadas também em disposições gráficas.
Leia mais: Aprenda a fazer um BoxPlot com Khan Academy!!
Conclusão
Esse tipo de gráfico é amplamente utilizado em apresentação de estudos, análise de dados e cálculos como forma de acelerar a compreensão de estudos de casos e avaliações estatísticas.
Portanto, é fundamental utilizar dados precisos, softwares e profissionais competentes para a realização do diagrama.